题目内容
16.两个相似三角形的面积比是4:9,其周长之比为( )| A. | 4:9 | B. | 2:3 | C. | 5:4 | D. | 1:2 |
分析 根据相似三角形(多边形)的周长的比等于相似比和相似三角形的面积的比等于相似比的平方求解.
解答 解:相似三角形的周长之比=$\sqrt{4}$:$\sqrt{9}$=2:3.
故选B.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形(多边形)的周长的比等于相似比;相似三角形的面积的比等于相似比的平方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.-a一定是( )
| A. | 正数 | B. | 负数 | C. | 零 | D. | 正数或零或负数 |
1. 如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )
如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )
 如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )
如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )| A. | 1 | B. | 2 | C. | 4 | D. | 3 |
6.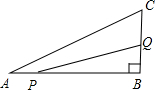 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,( )s后P、Q之间的距离等于4$\sqrt{2}$cm.
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,( )s后P、Q之间的距离等于4$\sqrt{2}$cm.
 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,( )s后P、Q之间的距离等于4$\sqrt{2}$cm.
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,( )s后P、Q之间的距离等于4$\sqrt{2}$cm.| A. | $\frac{2}{5}$ | B. | 2 | C. | $\frac{6}{5}$ | D. | $\frac{2}{5}$或2 |
 如图,已知AB∥FC,点E是DF的中点,AB=15,CF=8,求BD的长.
如图,已知AB∥FC,点E是DF的中点,AB=15,CF=8,求BD的长.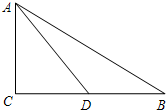 已知:如图,在Rt△ABC中,∠C=90°,AC=CD,∠B=30°,AD=2$\sqrt{2}$.
已知:如图,在Rt△ABC中,∠C=90°,AC=CD,∠B=30°,AD=2$\sqrt{2}$.