题目内容
6. 如图,已知AB∥FC,点E是DF的中点,AB=15,CF=8,求BD的长.
如图,已知AB∥FC,点E是DF的中点,AB=15,CF=8,求BD的长.
分析 利用AAS先证明△ADE≌△CFE,得AD=CF,再根据AB=15,求得BD的长即可.
解答 解:∵AB∥FC,
∴∠A=∠ECF,
∵点E是DF的中点,
∴DE=DF,
在△ADE和△CFE中,
$\left\{\begin{array}{l}{∠DAE=∠FCE}\\{∠DEA=∠FEC}\\{DE=FE}\end{array}\right.$,
∴△ADE≌△CFE(AAS),
∴AD=CF,
∵AB=15,CF=8,
∴BD=AB-AD=15-8=7,
∴BD的长为7.
点评 本题考查了全等三角形的判定和性质,正确证明三角形全等是关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
1.若△MNP≌△NMQ,且MN=8cm,NP=7cm,PM=6cm,则MQ的长为( )
| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
11.甲、乙两台机床同时加工直径为10mm的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取5件进行检测,结果如下(单位:mm):
(1)分别求出这两台机床所加工零件直径的平均数、极差和方差;
(2)哪一台机床生产零件的稳定性更好一些?为什么?
| 甲 | 10 | 9.8 | 10 | 10.2 | 10 |
| 乙 | 9.9 | 10 | 10 | 10.1 | 10 |
(2)哪一台机床生产零件的稳定性更好一些?为什么?
18.抛物线y=x2不具有的性质是( )
| A. | 对称轴是y轴 | B. | 开口向上 | ||
| C. | 当x<0时,y随x的增大而增大 | D. | 顶点坐标是(0,0) |
15.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用含x的代数式来表示销售量(件)和销售该品牌玩具获得利润(元),并把化简后的结果填写在表格中:
(2)在(1)问条件下,若商场获得了10000元销售利润,试问该玩具销售单价x应定为多少元?
(3)在(1)问条件下,商场有可能获得13000元的销售利润吗?若可能,请求出该玩具销售单价;若不可能,请说明理由.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用含x的代数式来表示销售量(件)和销售该品牌玩具获得利润(元),并把化简后的结果填写在表格中:
| 销售单价(元) | x |
| 销售量(件) | 1000-10x |
| 销售玩具获得利润(元) | -10x2+1300x-30000 |
(3)在(1)问条件下,商场有可能获得13000元的销售利润吗?若可能,请求出该玩具销售单价;若不可能,请说明理由.
16.两个相似三角形的面积比是4:9,其周长之比为( )
| A. | 4:9 | B. | 2:3 | C. | 5:4 | D. | 1:2 |
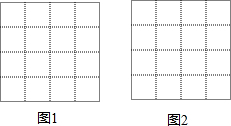 在图1、图2中的每个小正方形的边长都是1.
在图1、图2中的每个小正方形的边长都是1.