题目内容
1. 如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )
如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )| A. | 1 | B. | 2 | C. | 4 | D. | 3 |
分析 先证明△EDF∽△BCF,然后根据相似三角形的面积比等于相似比的平方求解即可.
解答 解:∵E为AD的中点,
∴DE=$\frac{1}{2}AD$.
∵四边形ABCD为平行四边形,
∴ED∥BC,AD=BC.
∴△EDF∽△BCF,DE=$\frac{1}{2}BC$.
∴$\frac{{S}_{△EDF}}{{S}_{△BCF}}=(\frac{ED}{BC})^{2}$,即$\frac{1}{{S}_{△BCF}}=\frac{1}{4}$.
∴S△BCF=4.
故选:C.
点评 本题主要考查的是相似三角形的性质,利用相似三角形的面积比等于相似比的平方求解是解题的关键.

练习册系列答案
相关题目
11.甲、乙两台机床同时加工直径为10mm的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取5件进行检测,结果如下(单位:mm):
(1)分别求出这两台机床所加工零件直径的平均数、极差和方差;
(2)哪一台机床生产零件的稳定性更好一些?为什么?
| 甲 | 10 | 9.8 | 10 | 10.2 | 10 |
| 乙 | 9.9 | 10 | 10 | 10.1 | 10 |
(2)哪一台机床生产零件的稳定性更好一些?为什么?
12.若a、b为有理数,a2=b2,则a、b的关系是( )
| A. | 相等 | B. | 互为相反数 | ||
| C. | 互为倒数 | D. | 相等或互为相反数 |
16.两个相似三角形的面积比是4:9,其周长之比为( )
| A. | 4:9 | B. | 2:3 | C. | 5:4 | D. | 1:2 |
13.一组数据3、18、10、12、17、4的中位数为( )
| A. | 3 | B. | 11 | C. | 12 | D. | 17 |
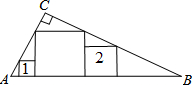 在Rt△ABC中,∠C=90°,现在其内部如图所示放置小、大、中三个正方形,其中小正方形边长为1,中正方形边长为2,则AC=$\frac{12\sqrt{5}}{5}$.
在Rt△ABC中,∠C=90°,现在其内部如图所示放置小、大、中三个正方形,其中小正方形边长为1,中正方形边长为2,则AC=$\frac{12\sqrt{5}}{5}$. 如图,楼梯形状图形的周长是36.
如图,楼梯形状图形的周长是36.