题目内容
8.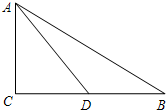 已知:如图,在Rt△ABC中,∠C=90°,AC=CD,∠B=30°,AD=2$\sqrt{2}$.
已知:如图,在Rt△ABC中,∠C=90°,AC=CD,∠B=30°,AD=2$\sqrt{2}$.求:线段DB的长.
分析 由等腰直角三角形的性质得出AC=CD=$\frac{\sqrt{2}}{2}$AD=2,由含30°角的直角三角形的性质得出AB=2AC=4,由勾股定理求出BC,即可得出DB的长.
解答 解:∵∠C=90°,AC=CD,
∴△ACD是等腰直角三角形,
∴AC=CD=$\frac{\sqrt{2}}{2}$AD=$\frac{\sqrt{2}}{2}$×2$\sqrt{2}$=2,
又∵∠B=30°,
∴AB=2AC=4.
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{3}$,
∴DB=BC-CD=2$\sqrt{3}$-2.
点评 本题考查了勾股定理、含30°角的直角三角形的性质、等腰直角三角形的性质,熟练掌握勾股定理,由勾股定理求出AC、BC是解决问题的关键.

练习册系列答案
相关题目
18.抛物线y=x2不具有的性质是( )
| A. | 对称轴是y轴 | B. | 开口向上 | ||
| C. | 当x<0时,y随x的增大而增大 | D. | 顶点坐标是(0,0) |
19.若不等式组$\left\{\begin{array}{l}x>7a+2\\ x<4a-7\end{array}\right.$无解,则a的取值范围是( )
| A. | a≥-3 | B. | a>-3 | C. | a≤-3 | D. | a<-3 |
16.两个相似三角形的面积比是4:9,其周长之比为( )
| A. | 4:9 | B. | 2:3 | C. | 5:4 | D. | 1:2 |
13.一组数据3、18、10、12、17、4的中位数为( )
| A. | 3 | B. | 11 | C. | 12 | D. | 17 |
18.下列运算正确的是( )
| A. | ${(\frac{2}{3})^2}=\frac{9}{2}$ | B. | ${(-\frac{3}{2})^3}=-\frac{27}{2}$ | C. | ${(-\frac{3}{2})^2}=-\frac{9}{4}$ | D. | ${(-\frac{3}{2})^3}=-\frac{27}{8}$ |