题目内容
 如图,点O是直线AB上的一点,OM是∠AOC的平分线,ON是∠COB的平分线,求∠MOC和∠NOC有何关系?为什么?
如图,点O是直线AB上的一点,OM是∠AOC的平分线,ON是∠COB的平分线,求∠MOC和∠NOC有何关系?为什么?解:∵OM是∠AOC的角平分线,
∴∠MOC=
| 1 |
| 2 |
∵ON是∠BOC的角平分线,
∴
| 1 |
| 2 |
∴∠MOC+∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠AOC+∠BOC=180°
∴∠MOC+∠NOC=
∴∠MOC与∠NOC
考点:角平分线的定义
专题:推理填空题
分析:由AB是一直线,即可求出∠AOB=180°,然后根据角平分线的性质,推出∠MOC=
∠AOC,∠NOC=
∠BOC,最后根据图形可知∠MON=∠MOC+NOC=
∠AOB=90°,∠MOC与∠NOC互余.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵OM是∠AOC的角平分线,
∴∠MOC=
∠AOC
∵ON是∠BOC的角平分线,
∴∠NOC=
∠BOC
∴∠MOC+∠NOC=
∠AOC+
∠BOC=
(∠AOC+∠BOC)
又∵∠AOC+∠BOC=180°
∴∠MOC+∠NOC=90°
∴∠MOC与∠NOC互余.
故答案为:∠AOC,∠NOC,90°,互余.
∴∠MOC=
| 1 |
| 2 |
∵ON是∠BOC的角平分线,
∴∠NOC=
| 1 |
| 2 |
∴∠MOC+∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠AOC+∠BOC=180°
∴∠MOC+∠NOC=90°
∴∠MOC与∠NOC互余.
故答案为:∠AOC,∠NOC,90°,互余.
点评:本题主要考查垂直的判定,角平分线的定义及性质,平角的概念及性质,关键在于运用数形结合的思想,结合角平分线的性质推出∠MON=∠MOC+∠NOC=
∠AOB.
| 1 |
| 2 |

练习册系列答案
相关题目
四个同学每两个人握一次手,一共握手多少次( )
| A、8 | B、4 | C、6 | D、10 |
下列各式中,变形不正确的是( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
解方程组
的最好解法是( )
|
| A、由①得y=3x-2,再代入② |
| B、由②得3x=11-2y,再代入① |
| C、由②-①,消去x |
| D、由①×2+②消去y |
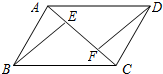 如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF,求证:△ABE≌△CDF.
如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF,求证:△ABE≌△CDF. 矩形ABCD中,点E是AD中点,EF⊥CE交AB于F,连CF.
矩形ABCD中,点E是AD中点,EF⊥CE交AB于F,连CF.