题目内容
10.解分式方程和一次不等式组(1)$\frac{5}{{{x^2}+3x}}-\frac{1}{{{x^2}-x}}=0$
(2)解不等式组:$\left\{\begin{array}{l}{x-3(x-1)≤7}\\{1-\frac{2-5x}{3}<x}\end{array}\right.$.
分析 (1)根据解分式方程的步骤,即可解答;
(2)先求出每一个不等式的解集,再确定不等式组的解集.
解答 解:(1)在方程两边同乘x(x+3)(x-1)得:5(x-1)-(x+3)=0,
解得:x=2,
检验:当x=2时,x(x+3)(x-1)≠0,
故x=2是分式方程的解.
(2)$\left\{\begin{array}{l}{x-3(x-1)≤7①}\\{1-\frac{2-5x}{3}<x②}\end{array}\right.$
由①得:x≥-2,
由②得:x<-$\frac{1}{2}$,
故不等式组的解集为:-2≤x<-$\frac{1}{2}$.
点评 本题考查了解分式方程和解一元一次不等式组,解决本题的关键是熟记解分式方程和解一元一次不等式组的步骤.

练习册系列答案
相关题目
15.如图是小李销售某种食品的总利润y元与销售量x千克的函数图象(总利润=总销售额-总成本).由于目前销售不佳,小李想了两个解决方案:
方案(1)是不改变食品售价,减少总成本;
方案(2)是不改变总成本,提高食品售价.
下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象,则分别反映了方案(1)(2)的图象是( )
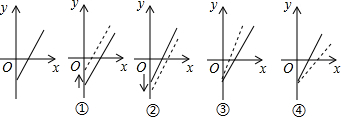
方案(1)是不改变食品售价,减少总成本;
方案(2)是不改变总成本,提高食品售价.
下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象,则分别反映了方案(1)(2)的图象是( )

| A. | ②,③ | B. | ①,③ | C. | ①,④ | D. | ④,② |
20.函数y=$\frac{1}{|x|}$的图象是( )
| A. |  | B. |  | C. |  | D. |  |