题目内容
2. 如图,在△ABC中,已知∠ABC=90°,AC=3,BC=4,以点B为中心将△ABC顺时针旋转,使点落在CB延长线上的点A1处,此时,点C落在点C1的位置,联结AA1、CC1交于点O,CC1与AB交于点D,AA1与BC1交于点E,求四边形BDOE的面积.
如图,在△ABC中,已知∠ABC=90°,AC=3,BC=4,以点B为中心将△ABC顺时针旋转,使点落在CB延长线上的点A1处,此时,点C落在点C1的位置,联结AA1、CC1交于点O,CC1与AB交于点D,AA1与BC1交于点E,求四边形BDOE的面积.
分析 过点C1作C1F⊥BA1于点F,由旋转的性质得到∠ABC=∠A1BC1,AB=A1B,BC=BC1,求得∠ABA1=∠CBC1,推出B,C,A,O四点共圆,连接BO,根据圆周角定理得到∠AOB=∠ACB=90°,AO=A1O,同理B,O,C1A1四点共圆,根据勾股定理得到AA1=$\sqrt{A{C}^{2}+C{{A}_{1}}^{2}}$=3$\sqrt{10}$,∴AO=$\frac{3}{2}$$\sqrt{10}$,推出△CDB∽△A1BE,同理△A1BE∽△ADO,设S△CDB=x,S四边形BDOE=y,则S${\;}_{△{A}_{1}EB}$$\frac{25}{16}$x,S△ADO=$\frac{45}{32}$x,于是得到S${\;}_{△AC{A}_{1}}$=$\frac{1}{2}$×3×(4+5)=$\frac{27}{2}$,由CO平分△ACA1的面积,得到S${\;}_{△CO{A}_{1}}$=$\frac{1}{2}$S${\;}_{△AC{A}_{1}}$=$\frac{27}{4}$,S${\;}_{△AB{A}_{1}}$=$\frac{1}{2}$×5×3=$\frac{15}{2}$,解方程组即可得到结论.
解答 解:由旋转的性质得:∠ABC=∠A1BC1,AB=A1B,BC=BC1,
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1,
∴∠OAB=∠OCB,
∴B,C,A,O四点共圆,
连接BO,
∴∠AOB=∠ACB=90°,AO=A1O,同理B,O,C1A1四点共圆,
∵∠ACB=90°,
∴AA1=$\sqrt{A{C}^{2}+C{{A}_{1}}^{2}}$=3$\sqrt{10}$,
∴AO=$\frac{3}{2}$$\sqrt{10}$,
∵∠ABC=∠A1BC1,∠DCB=∠DC1B=∠CA1E,
∴△CDB∽△A1BE,同理△A1BE∽△ADO,
设S△CDB=x,S四边形BDOE=y,
则S${\;}_{△{A}_{1}EB}$$\frac{25}{16}$x,S△ADO=$\frac{45}{32}$x,
∴S${\;}_{△AC{A}_{1}}$=$\frac{1}{2}$×3×(4+5)=$\frac{27}{2}$,
∵CO平分△ACA1的面积,
∴S${\;}_{△CO{A}_{1}}$=$\frac{1}{2}$S${\;}_{△AC{A}_{1}}$=$\frac{27}{4}$,S${\;}_{△AB{A}_{1}}$=$\frac{1}{2}$×5×3=$\frac{15}{2}$,
∴解方程组$\left\{\begin{array}{l}{(1+\frac{25}{16})x+y=\frac{27}{4}}\\{(\frac{25}{16}+\frac{45}{32})x+y=\frac{15}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{24}{13}}\\{y=\frac{105}{52}}\end{array}\right.$,
∴四边形BDOE的面积=$\frac{105}{52}$.
点评 本题考查了旋转的性质,相似三角形的判定和性质,三角形面积的计算,四点共圆,熟练掌握旋转的性质是解题的关键.

 名校课堂系列答案
名校课堂系列答案①等角的余角相等;
②一个角的补角一定大于这个角;
③有理数分为正数和负数;
④零是最小的正数;
⑤过直线外一点可以作一条以上的直线与已知直线平行.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 三个点确定一个圆 | |
| B. | 同弧所对的圆周角与圆心角相等 | |
| C. | 直径是圆中最长的弦 | |
| D. | 圆是轴对称图形,不是中心对称图形 |
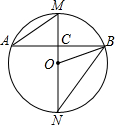 如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.
如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.