题目内容
3.在菱形ABCD中,∠BAD=60°,AB=1,此时称为图形L(1),连接图形L(1)的各边中点,得图形J(1),再连接图形J(1)各边中点得图形L(2),在连接图形L(2)各边中点得图形J(2),以此类推…,则图形L(n)的边长与图形J(n)的宽的和是$\frac{3}{{2}^{n}}$.分析 连接BD,由菱形的性质得出AB=AD,证明△ABD是等边三角形,得出BD=AB=1,证明EH是△ABD的中位线,得出EH=$\frac{1}{2}$BD=$\frac{1}{2}$,得出AB+EH=$\frac{3}{2}$,同理:MN=$\frac{1}{2}$AB=$\frac{1}{2}$,RT=$\frac{1}{4}$,得出MN+RT=$\frac{3}{{2}^{2}}$,…,得出规律:图形L(n)的边长与图形J(n)的宽的和=$\frac{1}{{2}^{n-1}}$+$\frac{1}{{2}^{n}}$=$\frac{3}{{2}^{n}}$.
解答 解:连接BD,如图所示: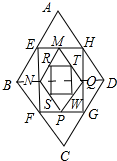 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=1,
∵E、H分别是AB、AD的中点,
∴EH是△ABD的中位线,
∴EH=$\frac{1}{2}$BD=$\frac{1}{2}$,
∴AB+EH=1+$\frac{1}{2}$=$\frac{3}{2}$,
同理:MN=$\frac{1}{2}$AB=$\frac{1}{2}$,RT=$\frac{1}{4}$,
∴MN+RT=$\frac{1}{2}$+$\frac{1}{4}$=$\frac{3}{4}$=$\frac{3}{{2}^{2}}$,…,
图形L(n)的边长与图形J(n)的宽的和=$\frac{1}{{2}^{n-1}}$+$\frac{1}{{2}^{n}}$=$\frac{3}{{2}^{n}}$;
故答案为:$\frac{3}{{2}^{n}}$.
点评 本题考查了菱形的性质、等边三角形的判定与性质、三角形中位线定理;熟练掌握菱形的性质,根据题意得出规律是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案 如图所示的物体是一个实心几何体,其俯视图是( )
如图所示的物体是一个实心几何体,其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
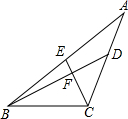 已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )| A. | $\frac{16}{3}$ | B. | 8 | C. | 4 | D. | 6 |
| A. |  锐角 | B. |  等腰三角形 | C. |  直角三角形 | D. |  扇形 |
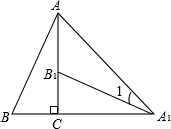 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是60°.
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是60°.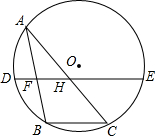 如图,点A是⊙O上一动点,BC是⊙O的一条弦,且∠BAC=30°,点F、H分别是AB、AC的中点,直线FH与⊙O交于D、E两点.若DF+EH的最大值是12,则⊙O的半径是8.
如图,点A是⊙O上一动点,BC是⊙O的一条弦,且∠BAC=30°,点F、H分别是AB、AC的中点,直线FH与⊙O交于D、E两点.若DF+EH的最大值是12,则⊙O的半径是8.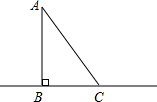 如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB=11.9m(用计算器计算,结果精确到0.1米)
如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB=11.9m(用计算器计算,结果精确到0.1米)