题目内容
8.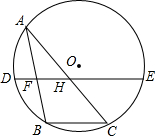 如图,点A是⊙O上一动点,BC是⊙O的一条弦,且∠BAC=30°,点F、H分别是AB、AC的中点,直线FH与⊙O交于D、E两点.若DF+EH的最大值是12,则⊙O的半径是8.
如图,点A是⊙O上一动点,BC是⊙O的一条弦,且∠BAC=30°,点F、H分别是AB、AC的中点,直线FH与⊙O交于D、E两点.若DF+EH的最大值是12,则⊙O的半径是8.
分析 由点E、F分别是AB、AC的中点,根据三角形中位线定理得出FH=$\frac{1}{2}$BC,则DF+EH=DE-FH=GH-3.5,所以当GH取最大值时,GE+FH有最大值.而直径是圆中最长的弦,故当GH为⊙O的直径时,DF+EH有最大值12.
解答 解:设该圆的半径是r.
当DE为⊙O的直径时,DF+EH有最大值.
当DE为直径时,H点与O点重合,
∴AC也是直径,AC=2r.
∵∠ABC是直径上的圆周角,
∴∠ABC=90°,
∵∠BAC=30°,
∴BC=$\frac{1}{2}$AC=r.
∵点F、H分别是AB、AC的中点,
∴FH=$\frac{1}{2}$BC=$\frac{1}{2}$r,
∴DF+EH=DE-FH=2r-$\frac{1}{2}$r=12.
解得r=8.
故答案为:8.
点评 本题结合动点考查了圆周角定理,三角形中位线定理,有一定难度.确定GH的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.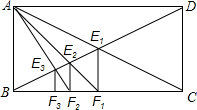 如图,矩形ABCD中,BC=1,连接AC与BD交于点E1,过E1作E1F1⊥BC于F1,连接AF1交BD于E2,过E2作E2F2⊥BC于F2,连接AF2交BD于E3,过E3作E3F3⊥BC于F3,…,以此类推,则BFn(其中n为正整数)的长为( )
如图,矩形ABCD中,BC=1,连接AC与BD交于点E1,过E1作E1F1⊥BC于F1,连接AF1交BD于E2,过E2作E2F2⊥BC于F2,连接AF2交BD于E3,过E3作E3F3⊥BC于F3,…,以此类推,则BFn(其中n为正整数)的长为( )
 如图,矩形ABCD中,BC=1,连接AC与BD交于点E1,过E1作E1F1⊥BC于F1,连接AF1交BD于E2,过E2作E2F2⊥BC于F2,连接AF2交BD于E3,过E3作E3F3⊥BC于F3,…,以此类推,则BFn(其中n为正整数)的长为( )
如图,矩形ABCD中,BC=1,连接AC与BD交于点E1,过E1作E1F1⊥BC于F1,连接AF1交BD于E2,过E2作E2F2⊥BC于F2,连接AF2交BD于E3,过E3作E3F3⊥BC于F3,…,以此类推,则BFn(其中n为正整数)的长为( )| A. | $\frac{n}{n+1}$ | B. | $\frac{1}{n+1}$ | C. | $\frac{n+1}{n+2}$ | D. | $\frac{n+1}{n+3}$ |
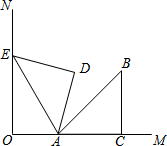 如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.
如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.