题目内容
2.结合数轴与绝对值的知识回答下列问题:(1)探究归纳:①数轴上表示5和2的两点之间的距离是3个单位长度;
②数轴上表示-2和-6的两点之间的距离是4个单位长度;
③数轴上表示-4和3的两点之间的距离是7个单位长度;
一般地,数轴上表示数m和数m的两点之间的距离等于|m-n|.
(2)应用:
①若数轴上表示数a的点位于-4与3之间,则|a+4|+|a-3|的值为7;
②当a=1,|a+4|+|a-1|+|a-3|的值最小,最小值是7.
分析 (1)根据题意和数轴的特点可以解答本题;
(2)根据数轴的特点和去绝对值的方法可以解答本题.
解答 解:(1)由题意可得,
①数轴上表示5和2的两点之间的距离是:5-2=3,
②数轴上表示-2和-6的两点之间的距离是:(-2)-(-6)=4,
③数轴上表示-4和3的两点之间的距离是:3-(-4)=7,
故答案为:3个单位长度,4个单位长度,7个单位长度;
(2)①∵数a的点位于-4与3之间,
∴|a+4|+|a-3|
=a+4+3-a
=7,
故答案为:7;
②当a≥3时
|a+4|+|a-1|+|a-3|
=a+4+a-1+a-3
=3a≥9,
当1≤a<3时,
|a+4|+|a-1|+|a-3|
=a+4+a-1+3-a
=a+6≥7,
当-4≤a≤1时,
|a+4|+|a-1|+|a-3|
=a+4+1-a+3-a
=-a+8≥7,
当a≤-4时,
|a+4|+|a-1|+|a-3|
=-a-4+1-a+3-a
=-3a≤12,
故答案为:①7;②1,7
点评 本题考查数轴、绝对值、整式的加减,解答此类问题的关键是明确数轴的特点,利用分类讨论的数学思想解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.如果x2+4xy+4y2=0,那么$\frac{x}{y}$的值为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
13.已知圆锥的底面半径为3cm,母线长为5cm,则圆锥的侧面积是( )
| A. | 20 cm2 | B. | 20π cm2 | C. | 15 cm2 | D. | 15π cm2 |
10.若最简二次根式$\sqrt{1+2a}$与2$\sqrt{3}$是同类二次根式,则a的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{5}{2}$ |
17.计算(ab2)4的结果,正确的是( )
| A. | a4b8 | B. | a4b6 | C. | ab8 | D. | ab6 |
11.某班的一次数学测验中,共出了20道选择题,每小题5分,总分为100分,答对加分,答错倒扣分.现从中抽出5份试卷进行分析,如表:
(1)甲同学得了76分,他答对了多少道题?
(2)有一位同学说“同学乙得了89分”,这个成绩准确吗?为什么?
| 试卷 | 正确个数 | 错误个数 | 得分 |
| A | 19 | 1 | 94 |
| B | 18 | 2 | 88 |
| C | 17 | 3 | 82 |
| D | 14 | 6 | 64 |
| E | 10 | 10 | 40 |
(2)有一位同学说“同学乙得了89分”,这个成绩准确吗?为什么?
12.如图,已知∠BAC=∠DAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )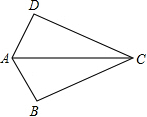

| A. | CB=CD | B. | AB=AD | C. | ∠BCA=∠DCA | D. | ∠B=∠D |
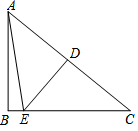 如图,在Rt△ABC中,∠B为直角,DE是AC的垂直平分线,DE交AC于点D,交BC于点E,且∠BAE:∠BAC=1:5,则∠C=40°.
如图,在Rt△ABC中,∠B为直角,DE是AC的垂直平分线,DE交AC于点D,交BC于点E,且∠BAE:∠BAC=1:5,则∠C=40°.