题目内容
10.某超市计划经销一些特产,经销前,围绕“A:绥中白梨,B:虹螺岘干豆腐,C:绥中六股河鸭蛋,D:兴城红崖子花生”四种特产,在全市范围内随机抽取了部分市民进行问卷调查:“我最喜欢的特产是什么?”(必选且只选一种).现将调查结果整理后,绘制成如图所示的不完整的扇形统计图和条形统计图.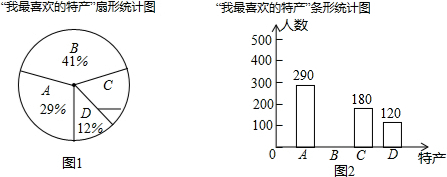
请根据所给信息解答以下问题:
(1)请补全扇形统计图和条形统计图;
(2)若全市有280万市民,估计全市最喜欢“虹螺岘干豆腐”的市民约有多少万人?
(3)在一个不透明的口袋中有四个分别写上四种特产标记A、B、C、D的小球(除标记外完全相同),随机摸出一个小球然后放回,混合摇匀后,再随机摸出一个小球,则两次都摸到“A”的概率为$\frac{1}{16}$.
分析 (1)根据A的人数与所占的百分比列式求出随机抽取的总人数,再求出B的人数,最后补全两个统计图即可;
(2)用全市的总人数乘以B所占的百分比,计算即可得解;
(3)画出树状图,然后根据概率公式列式计算即可得解.
解答 解:(1)被抽查的总人数:290÷29%=1000,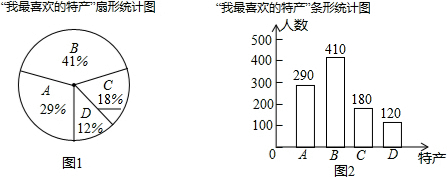
B的人数:1000-290-180-120=410,
C所占的百分比:180÷1000=18%;
(2)280×41%=114.8(万人),
答:最喜欢“虹螺岘干豆腐”的市民约有114.8万人;
(3)根据题意作出树状图如下: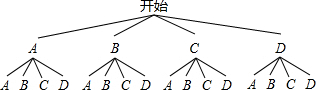
共有16种可能情况,并且发生的可能性相等,两次都摸到“A”的有1种情况,
所以P(A,A)=$\frac{1}{16}$.
故答案为:$\frac{1}{16}$.
点评 本题考查了列表法和树状图法,扇形统计图和条形统计图,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1. 如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于( )
如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于( )
 如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于( )
如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于( )| A. | 10° | B. | 20° | C. | 30° | D. | 50° |
5.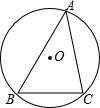 如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则$\widehat{BC}$的长是( )
如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则$\widehat{BC}$的长是( )
 如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则$\widehat{BC}$的长是( )
如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则$\widehat{BC}$的长是( )| A. | $\frac{3}{4}$π | B. | $\frac{3}{2}$π | C. | $\frac{45}{2}$π | D. | $\frac{9}{4}$π |
19.⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
| A. | 点A在圆上 | B. | 点A在圆内 | C. | 点A在圆外 | D. | 无法确定 |
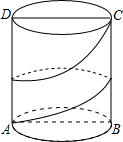 在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为3$\sqrt{{π}^{2}+1}$cm.(结果保留π)
在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为3$\sqrt{{π}^{2}+1}$cm.(结果保留π)