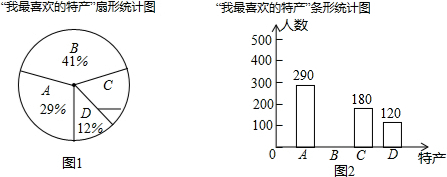
题目内容
18.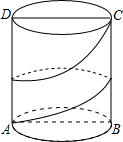 在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为3$\sqrt{{π}^{2}+1}$cm.(结果保留π)
在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为3$\sqrt{{π}^{2}+1}$cm.(结果保留π)
分析 根据绕两圈到C,则展开后相当于求出直角三角形ACB的斜边长,并且AB的长为圆柱的底面圆的周长的1.5倍,BC的长为圆柱的高,根据勾股定理求出即可.
解答 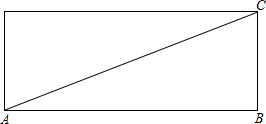 解:如图所示,
解:如图所示,
∵无弹性的丝带从A至C,绕了1.5圈,
∴展开后AB=1.5×2π=3πcm,BC=3cm,
由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{9{π}^{2}+9}$=3$\sqrt{{π}^{2}+1}$cm.
故答案为:3$\sqrt{{π}^{2}+1}$.
点评 本题考查了平面展开-最短路线问题和勾股定理的应用,能正确画出图形是解此题的关键,用了数形结合思想.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
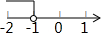
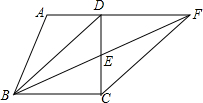 如图,四边形ABCD中,AD∥BC,E是DC上一点,连接BE并延长交AD延长线于点F,请你只添加一个条件:BD∥FC使得四边形BDFC为平行四边形.
如图,四边形ABCD中,AD∥BC,E是DC上一点,连接BE并延长交AD延长线于点F,请你只添加一个条件:BD∥FC使得四边形BDFC为平行四边形.


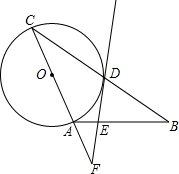 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.