题目内容
如图,有一个圆锥形的粮堆,其轴截面是边长为6 m的正三角形ABC,圆锥的母线AC的中点P处有一个老鼠在偷吃粮食,此时小猫正在B处,它要沿圆锥侧面到达P处捕鼠,则小猫所经过 的最短路程为( )
的最短路程为( )
(A) m (B)
m (B) m (C)
m (C) m (D)
m (D) m
m

B.此圆锥的侧面展开图为扇形(如图 ),由题意知,底面圆的直径BC=6 m,
),由题意知,底面圆的直径BC=6 m, 故底面的周长等于6π m,设圆锥侧面展开后扇形的圆心角为n°,因为底面的
故底面的周长等于6π m,设圆锥侧面展开后扇形的圆心角为n°,因为底面的 周长等于展开后扇形的弧长,且AB=6 m,所以6π=
周长等于展开后扇形的弧长,且AB=6 m,所以6π= 得n=180,在Rt△AB′P中,易得B′P=
得n=180,在Rt△AB′P中,易得B′P= (m),所以小猫所经过的最短路程为
(m),所以小猫所经过的最短路程为 m.
m.

【归纳整合】最短路线问题解题策略
空间图形求表面上路线最小值时,关键是弄清几何体中的有关点、线在展开图中的相应位置关系.解决的方法就是把各侧面展开铺在平面上,根据“两点之间,线段最短”的方法来解决.

练习册系列答案
相关题目
 ,x1x2=
,x1x2= .例如:若x1,x2是方程2x2-x-1=0的两个根,则x1+x2=-
.例如:若x1,x2是方程2x2-x-1=0的两个根,则x1+x2=- =
= +
+ 的值
的值
 (3)如果视力在4.9~5.1(含4.9,5.1)均属正常,则全市有 名初中生的视力正常, 视力正常的合格率是 .
(3)如果视力在4.9~5.1(含4.9,5.1)均属正常,则全市有 名初中生的视力正常, 视力正常的合格率是 .  cm,侧面展开图是半圆.
cm,侧面展开图是半圆. 在平面直角坐标系的第四象限内,则α的取值范围为 ( )
在平面直角坐标系的第四象限内,则α的取值范围为 ( ) B.
B. C.
C. D.
D.
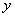 轴相切于点C(0,4),与
轴相切于点C(0,4),与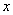 轴相交于A、B两点,且AB=6.
轴相交于A、B两点,且AB=6. ACB= ;经过C、A、B三点的抛物线的解析式 ;
ACB= ;经过C、A、B三点的抛物线的解析式 ; 面积最大,最大值是多少,并求出
面积最大,最大值是多少,并求出 点坐标.
点坐标.
 ,其中x=4
,其中x=4