题目内容
 如图,在平面直角坐标系中,点O是坐标原点,点A的坐标为(-1,2),点B坐标为(-2,0).
如图,在平面直角坐标系中,点O是坐标原点,点A的坐标为(-1,2),点B坐标为(-2,0).(1)在图中画出A、B点;
(2)画出△OAB,并将△OAB沿x轴向右平移2个单位后,得到△O1A1B1,画出平移后的△O1A1B1,并写出其三个顶点的坐标:
O1
(3)求△OAB的面积.
考点:作图-平移变换
专题:
分析:(1)利用平面直角坐标系得出A,B点位置;
(2)利用平移的性质得出平移后对应点坐标;
(3)利用A点坐标,结合三角形面积公式求出即可.
(2)利用平移的性质得出平移后对应点坐标;
(3)利用A点坐标,结合三角形面积公式求出即可.
解答:解: (1)如图所示:
(1)如图所示:
(2)如图所示:△O1A1B1,并写出其三个顶点的坐标:
O1 (2,0)A1 (1,2)B1 (0,0),
故答案为:(2,0)(1,2)(0,0);
(3)S△AOB=
×2×2=2.
 (1)如图所示:
(1)如图所示:(2)如图所示:△O1A1B1,并写出其三个顶点的坐标:
O1 (2,0)A1 (1,2)B1 (0,0),
故答案为:(2,0)(1,2)(0,0);
(3)S△AOB=
| 1 |
| 2 |
点评:此题主要考查了平移变换以及三角形面积求法,利用平移规律得出对应点坐标是解题关键.

练习册系列答案
相关题目
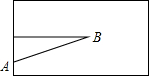 如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,这次小明的跳远成绩是4.6米,则小明从起跳点到落脚点之间的距离是( )
如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,这次小明的跳远成绩是4.6米,则小明从起跳点到落脚点之间的距离是( )| A、大于4.6米 |
| B、等于4.6米 |
| C、小于4.6米 |
| D、不能确定 |
已知a<b,下列四个不等式中不正确的是( )
| A、3a<3b |
| B、-3a>-3b |
| C、a+3<b+3 |
| D、2-a<2-b |
定义一种新运算“*”,规定:a*b=
a-4b,则12*(-1)=( )
| 1 |
| 3 |
| A、-8 | B、8 | C、-12 | D、11 |

 如图,E是△ABC边AC上一点,O为BE的中点,过点B作AC的平行线与AO的延长线相交于点D,连接DE,那么DE与AB有怎样的数量和位置关系?
如图,E是△ABC边AC上一点,O为BE的中点,过点B作AC的平行线与AO的延长线相交于点D,连接DE,那么DE与AB有怎样的数量和位置关系?