题目内容
17.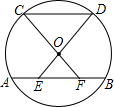 如图,AB、CD为⊙O的弦,且AB∥CD,连接CO并延长交AB于F,连接DO并延长交AB于E两点,求证:AE=BF.
如图,AB、CD为⊙O的弦,且AB∥CD,连接CO并延长交AB于F,连接DO并延长交AB于E两点,求证:AE=BF.
分析 过O作OH⊥AB于H,由垂径定理得出AH=BH,由等腰三角形的性质和平行线的性质得出∠OFE=∠OEF,证出OE=OF,由等腰三角形的三线合一性质得出EH=FH,即可得出结论.
解答 证明:过O作OH⊥AB于H,如图所示:
则AH=BH,
∵OC=OD,
∴∠C=∠D,
∵CD∥AB,
∴∠C=∠OFE,∠D=∠OEF,
∴∠OFE=∠OEF,
∴OE=OF,
∵OH⊥AB,
∴EH=FH,
∴AH-EH=BH-FH,
∴AE=BF.
点评 本题考查了垂径定理、等腰三角形的性质、平行线的性质;熟练掌握垂径定理,证明三角形是等腰三角形是解决问题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
7.以下各数中,填入□中能使(-$\frac{1}{2}$)×□=-2成立的是( )
| A. | -1 | B. | 2 | C. | 4 | D. | -4 |
5.为执行“均衡教育”政策,某县2014年投入教育经费2500万元,预计到2016年底三年累计投入1.2亿元.若每年投入教育经费的年平均增长 百分率为x,则下列方程正确的是( )
| A. | 2500(1+x)2=1.2 | B. | 2500(1+x)2=12000 | ||
| C. | 2500+2500(1+x)+2500(1+x)2=1.2 | D. | 2500+2500(1+x)+2500(1+x)2=12000 |
12.近几年安徽省民生事业持续改善,2012年全省民生支出3163亿元,2014年全省民生支出4349亿元,若平均每年民生支出的增长率相同,设这个增长率为x,则下列列出的方程中正确的是( )
| A. | 3163(1+x)2=4349 | B. | 4349(1-x)2=3163 | C. | 3163(1+2x)=4349 | D. | 4349(1-2x)=3163 |
2.据统计,2015年目前安徽的人口达到约69285000人,用科学记数法表示为( )
| A. | 6.9285×108 | B. | 69.285×106 | C. | 0.69285×108 | D. | 6.9285×107 |
 ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为4a-8b.
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为4a-8b.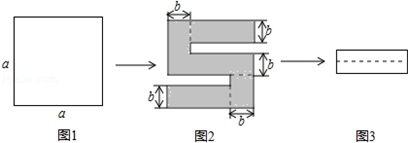
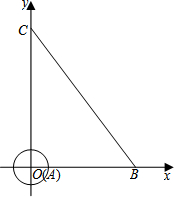 如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=$\frac{3}{5}$.
如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=$\frac{3}{5}$.