题目内容
6.在平面直角坐标系xOy中,已知点A、B、C的坐标分别为A(1,0)、B(3,1)、C(3,5),则三角形ABC的面积为4.分析 根据B和C的横坐标相同,则BC与x轴平行,据此即可求得BC的长,然后根据三角形的面积公式即可求解.
解答 解:BC=5-1=4,
则△ABC的面积是$\frac{1}{2}$×4×2=4.
故答案是:4.
点评 本题考查了三角形的面积公式和点的坐标,理解BC与x轴平行,确定三角形的面积公式是关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
16.连掷两次骰子,它们的点数都是3的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{36}$ | D. | $\frac{1}{4}$ |
11.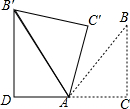 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
15.已知二次函数y=x2-6x+m的最小值是-3,那么m的值等于( )
| A. | 10 | B. | 4 | C. | 5 | D. | 6 |
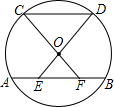 如图,AB、CD为⊙O的弦,且AB∥CD,连接CO并延长交AB于F,连接DO并延长交AB于E两点,求证:AE=BF.
如图,AB、CD为⊙O的弦,且AB∥CD,连接CO并延长交AB于F,连接DO并延长交AB于E两点,求证:AE=BF.