题目内容
7.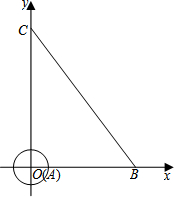 如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=$\frac{3}{5}$.
如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=$\frac{3}{5}$.(1)若点Q是线段BC上一点,且点Q的横坐标为m.
①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.
①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.
分析 (1)①根据正切的概念求出BC=10,OC=8,运用待定系数法求出直线BC的解析式,根据函数图象上点的坐标特征解得即可;
②作OQ⊥AB交⊙A于P,则此时PQ最小,根据三角形面积公式计算即可;
(2)①根据切线的性质和相似三角形的性质计算即可;
②结合图形、运用直线与圆的位置关系定理解答.
解答  解:(1)①∵点B的坐标为(6,0),tan∠OCB=$\frac{3}{5}$,
解:(1)①∵点B的坐标为(6,0),tan∠OCB=$\frac{3}{5}$,
∴BC=10,OC=8,
设直线BC的解析式为y=kx+b,
$\left\{\begin{array}{l}{6k+b=0}\\{b=8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=8}\end{array}\right.$,
∵点Q的横坐标为m,
∴点Q的纵坐标为-$\frac{4}{3}$m+8;
②如图1,作OQ⊥AB交⊙A于P,则此时PQ最小,
$\frac{1}{2}$×AB×OQ=$\frac{1}{2}$×BO×CO,
解得,OQ=4.8,
∴PQ最小=OQ最小-1=3.8;
(2)①如图2, ⊙A与直线BC相切于H,
⊙A与直线BC相切于H,
则AH⊥BC,又∠BOC=90°,
∴△BHA∽△BOC,
∴$\frac{BA}{BC}$=$\frac{AH}{OC}$,即$\frac{BA}{10}$=$\frac{1}{8}$,
解得,BA=$\frac{5}{4}$,
则OA=6-$\frac{5}{4}$=$\frac{19}{4}$,
∴t=$\frac{19}{4}$时,⊙A与直线BC相切;
②由(2)①得,t=$\frac{19}{4}$时,⊙A与直线BC相切,
当t=5时,⊙A经过点B,
当t=7时,⊙A经过点B,
当t=15时,⊙A经过点C,
故$\frac{19}{4}$<t≤5或7≤t≤15时,⊙A与线段BC有两个公共点.
点评 本题考查的是直线与圆的位置关系、待定系数法求一次函数的解析式以及最短距离的确定,灵活运用相关定理和数形结合思想是解题的关键.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | 10 | B. | 4 | C. | 5 | D. | 6 |
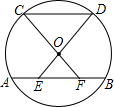 如图,AB、CD为⊙O的弦,且AB∥CD,连接CO并延长交AB于F,连接DO并延长交AB于E两点,求证:AE=BF.
如图,AB、CD为⊙O的弦,且AB∥CD,连接CO并延长交AB于F,连接DO并延长交AB于E两点,求证:AE=BF.
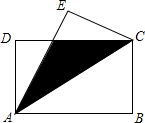 如图,ABCD是长方形,AB=8,BC=6,若将△ABC沿AC对折过来,则B点落到E处,AE交CD于F,求重叠部分的面积.
如图,ABCD是长方形,AB=8,BC=6,若将△ABC沿AC对折过来,则B点落到E处,AE交CD于F,求重叠部分的面积.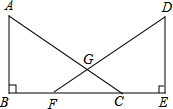 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:AB=DE.
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:AB=DE.