题目内容
11.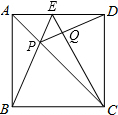 如图,已知正方形ABCD,E为AD的中点,连接BE和EC,BE交AC于点P,连接DP,交CE于Q.求证:
如图,已知正方形ABCD,E为AD的中点,连接BE和EC,BE交AC于点P,连接DP,交CE于Q.求证:(1)△ABP≌△ADP;
(2)DP⊥CE.
分析 (1)利用“SAA”即可证明△ABP≌△ADP;
(2)若要证明DP⊥CE,则问题可转化为证明∠EQD=90°即可.
解答 证明:
(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP=45°,
在△ABP和△ADP中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAP=∠DAP=45°}\\{AP=AP}\end{array}\right.$,
∴△ABP≌△ADP;
(2)∵E为AD的中点,
∴AE=DE,
在△AEB和△CDE中
$\left\{\begin{array}{l}{AB=DC}\\{∠BAE=∠CDE=90°}\\{AE=DE}\end{array}\right.$,
∴△AEB≌△CDE,
∴∠DEC=∠AEB,
∵∠ABE+∠AEB=90°,
∴∠ADP+∠DEC=90°,
∴∠EQD=90°,
即DP⊥CE.
点评 本题考查了正方形的性质以及全等三角形的判定和性质,得出∠EQD=90°是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列命题中,正确的是( )
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 有一个角为90°的四边形是平行四边形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线相等的菱形是正方形 |
16.把多项式x2-x提取公因式x后,余下的部分是( )
| A. | x | B. | x-1 | C. | x+1 | D. | x2 |
1.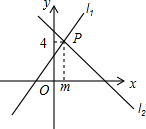 如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( )
如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( )
 如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( )
如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( )| A. | x≥4 | B. | x<m | C. | x≥m | D. | x≤1 |
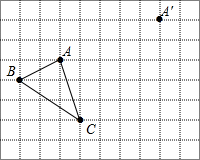 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点.