题目内容
10. 如图,在半径为2的⊙O中,AB=2$\sqrt{3}$,CD=2$\sqrt{2}$,AB与CD交于点E,延长AC、DB交于点F,则∠F=75°.
如图,在半径为2的⊙O中,AB=2$\sqrt{3}$,CD=2$\sqrt{2}$,AB与CD交于点E,延长AC、DB交于点F,则∠F=75°.
分析 作辅助线,根据直径所对的圆周角是90°,得到直角△ABH和直角△CDG,利用勾股定理计算DG和BH的长,得到∠CGD=45°,∠HAB=30°,再利用四点共圆的性质得∠DCF=∠DGA,再根据同弧所对的圆周角相等和三角形的内角和求出∠F的度数.
解答 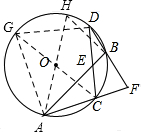 解:作直径CG、AH,交⊙O于G、H,连接AG、DG、BH,
解:作直径CG、AH,交⊙O于G、H,连接AG、DG、BH,
∴∠CDG=∠ABH=90°,
∵AB=2$\sqrt{3}$,CD=2$\sqrt{2}$,CG=AH=4,
由勾股定理得:DG=$\sqrt{C{G}^{2}-C{D}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{2}$,
BH=$\sqrt{A{H}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,
∴DG=CD,BH=$\frac{1}{2}$AH,
∴∠CGD=45°,∠HAB=30°,
∴∠AHB=60°,
∵A、C、D、G四点共圆,
∴∠DCF=∠DGA=∠AGC+∠CGD=∠AGC+45°,
∵∠AHB=∠AGC+∠CDF,∠CDF=∠FAB,
∴∠AHB=∠AGC+∠FAB=60°,
在△DCF中,∠F=180°-∠DCF-∠CDF,
=180°-∠AGC-45°-∠FAB,
=180°-45°-60°,
=75°,
故答案为:75°.
点评 本题考查了圆周角定理和四点共圆的性质,熟知在同圆或等圆中:①直径所对的圆周角是90°,②同弧所对的圆周角相等,圆内接四边形的对角互补;本题还运用勾股定理求边长,利用边的特殊关系得到等腰直角三角形和30°的直角三角形,从而得出结论.

练习册系列答案
相关题目
15.下列二次根式属于最简二次根式的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{48}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{4a+4}$ |
 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围. 如图,正方形ABCD,点E是DC上一点,点F是AD上一点,且AF>DF,EF=EC,FG⊥EF交AB于点G,连接CF、CG,若△CFG的面积为15,BC=6,则AF的长度是4.
如图,正方形ABCD,点E是DC上一点,点F是AD上一点,且AF>DF,EF=EC,FG⊥EF交AB于点G,连接CF、CG,若△CFG的面积为15,BC=6,则AF的长度是4.