题目内容
18.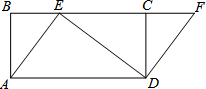 如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE.
如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE.(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
分析 (1)直接利用矩形的性质结合全等三角形的判定与性质得出BE=CF,进而得出答案;
(2)利用勾股定理的逆定理得出∠EDF=90°,进而得出$\frac{1}{2}$•ED•DF=$\frac{1}{2}$EF•CD,求出答案即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠B=∠DCF=90°,
∵∠BAE=∠CDF,
在△ABE和△DCF中,
$\left\{\begin{array}{l}{∠B=∠DCF}\\{AB=DC}\\{∠BAE=∠CDF}\end{array}\right.$,
∴△ABE≌△DCF(ASA),
∴BE=CF,
∴BC=EF,
∵BC=AD,
∴EF=AD,
又∵EF∥AD,
∴四边形AEFD是平行四边形;
(2)解:由(1)知:EF=AD=5,
在△EFD中,∵DF=3,DE=4,EF=5,
∴DE2+DF2=EF2,
∴∠EDF=90°,
∴$\frac{1}{2}$•ED•DF=$\frac{1}{2}$EF•CD,
∴CD=$\frac{12}{5}$.
点评 此题主要考查了矩形的性质以及勾股定理的逆定理,得出BC=EF是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.初三(8)班体委用划记法统计本班40名同学投掷实心球的成绩,结果如下表所示:
则这40名同学投掷实心球的成绩的众数和中位数分别是( )
| 成绩(分) | 6 | 7 | 8 | 9 | 10 |
| 人数 |  | 正 一 | 正 正 一 | 正 正  | 正 |
| A. | 9,8 | B. | 9,8.5 | C. | 8,8 | D. | 8,8.5 |
7.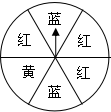 如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是( )
如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是( )
 如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是( )
如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
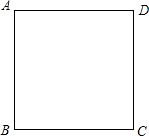 正方形、等边三角形是常见的轴对称图形.如图,设有一个边长为1的正方形ABCD,试在这个正方形中找出一个面积最大的和一个面积最小的内接等边三角形,并求出这两个图形的面积.
正方形、等边三角形是常见的轴对称图形.如图,设有一个边长为1的正方形ABCD,试在这个正方形中找出一个面积最大的和一个面积最小的内接等边三角形,并求出这两个图形的面积.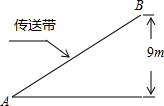 如图,传送带和地面所成的斜坡的坡度为1:$\sqrt{3}$,它把物体从地面送到离地面9米高的地方,则物体从A到B所经过的路程为18米.
如图,传送带和地面所成的斜坡的坡度为1:$\sqrt{3}$,它把物体从地面送到离地面9米高的地方,则物体从A到B所经过的路程为18米.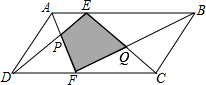 如图,在?ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为41cm2.
如图,在?ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为41cm2.