题目内容
8.如图1,在菱形ABCD中,E是CD上的一点,连接BE交AC于O,连接DO并延长交BC于F.(1)求证:△FOC≌△EOC.
(2)将此图中的AD、BE分别延长交于点N,作EM∥BC交CN于M,再连接FM即得到图2.
求证:①$\frac{CF}{CB}=\frac{BE}{BN}$;②FD=FM.
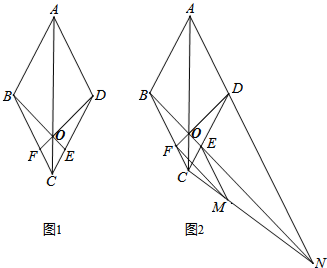
分析 (1)可以通过多组三角形全等证得,先根据SAS证明△BCO≌△DCO,得到∠CBO=∠CDO,然后根据ASA证明△BEC≌△DFC,进而可得CF=CE,然后根据SAS即可证明△FOC≌△EOC;
(2)利用EM∥BC来转化比:$\frac{BE}{BN}=\frac{CM}{CN}$,由BC∥AD,可得EM∥AD,可得$\frac{CM}{CN}=\frac{CE}{CD}$,进而可得:$\frac{CE}{CD}=\frac{BE}{BN}$,再利用CE=CF,CD=CB,即可得证$\frac{CF}{CB}=\frac{BE}{BN}$;
由$\frac{CM}{CN}=\frac{CF}{CB}$,得到FM∥BN,再利用EM∥BC,得到四边形FMEB为平行四边形,从而FM=BE=FD.
解答 (1)证明:∵四边形ABCD是菱形,
∴BC=CD,∠BCA=∠DCA,BC∥AD,
在△BCO和△DCO中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCA=∠DCA}\\{OC=OC}\end{array}\right.$,
∴△BCO≌△DCO(SAS),
∴∠CBO=∠CDO,
在△BEC和△DFC中,
$\left\{\begin{array}{l}{∠CBO=∠CDO}\\{BC=CD}\\{∠BCE=∠DCF}\end{array}\right.$,
∴△BEC≌△DFC(ASA),
∴EC=FC,
在△FOC和△EOC中,
$\left\{\begin{array}{l}{FC=EC}\\{∠BCA=∠DCA}\\{OC=OC}\end{array}\right.$,
∴△FOC≌△EOC(SAS);
(2)如图2所示,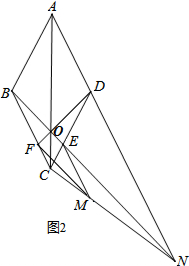
∵EM∥BC,BC∥AD,
∴EM∥BC∥AD
∴$\frac{BE}{BN}=\frac{CM}{CN}$,$\frac{CM}{CN}=\frac{CE}{CD}$,
∴$\frac{CE}{CD}=\frac{BE}{BN}$,
∵CE=CF,CD=CB
∴$\frac{CM}{CN}=\frac{CF}{CB}$,
∴$\frac{CF}{CB}=\frac{BE}{BN}$;
∵$\frac{CM}{CN}=\frac{CF}{CB}$
∴FM∥BN
∵EM∥BC
∴四边形FMEB为平行四边形
∴FM=BE
∵BE=DF
∴FD=FM.
点评 此题考查了全等三角形判定与性质及平行线分线段成比例定理,解题的关键是:利用EM∥BC∥AD来转化比:$\frac{BE}{BN}=\frac{CM}{CN}$,$\frac{CM}{CN}=\frac{CE}{CD}$,进而可得:$\frac{CE}{CD}=\frac{BE}{BN}$.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案| A. | “任意画出一个等边三角形,它是轴对称图形”是随机事件 | |
| B. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 | |
| C. | “概率为0.0001的事件”是不可能事件 | |
| D. | 任意掷一枚质地均匀的硬币10次,正面向上的一定是5次 |

 观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.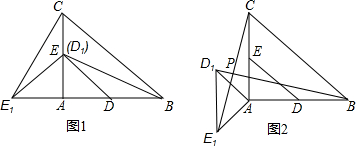
 如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)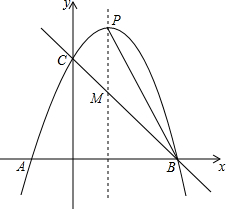 如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.