题目内容
10.在平面直角坐系中,O为坐标原点,点A的坐标为(1,1).点C在x轴上,且OA=AC,点D为x轴上一动点,连接AD,将线段AD绕点A按逆时针方向旋转90°,得到线段AD′,若CD′=$\sqrt{2}$,则CD的长为2+$\sqrt{2}$或2-$\sqrt{2}$.分析 根据点A的坐标可求得AO、AC的长,再结合旋转的性质,判定△DAO≌△D'AC(SAS),得出DO=D'C=$\sqrt{2}$,最后分两种情况讨论,求得CD的长.
解答 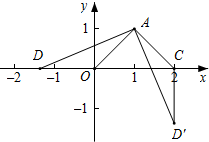 解:∵点A的坐标为(1,1),
解:∵点A的坐标为(1,1),
∴AO=$\sqrt{2}$=AC,OC=2,∠OCA=90°.
∵线段AD绕点A按逆时针方向旋转90°得到线段AD′,
∴AD=AD',∠DAD'=90°,
∴∠DAO=∠D'AC,
在△DAO和△D'AC中,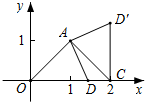
$\left\{\begin{array}{l}{AD=AD'}\\{∠DAO=∠D'AC}\\{OA=CA}\end{array}\right.$,
∴△DAO≌△D'AC(SAS)
∴DO=D'C=$\sqrt{2}$,
分两种情况:
①如图,当D在原点O左侧时,CD=CO+DO=2+$\sqrt{2}$;
②如图,当D在原点O右侧时,CD=CO-DO=2-$\sqrt{2}$;
故答案为:2+$\sqrt{2}$或2-$\sqrt{2}$.
点评 本题主要考查了旋转的性质以及全等三角形的判定,解决问题的关键是分类讨论思想的运用,在解题时需要画出图形进行分析,做到不重复不遗漏.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
1.三角形的三边长分别是3,1+2a,8,则数a的取值范围是( )
| A. | -2<a<4 | B. | 1<a<3.5 | C. | 2<a<5 | D. | 4<a<5 |
18. 在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDC的面积为( )
在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDC的面积为( )
 在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDC的面积为( )
在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDC的面积为( )| A. | 2$\sqrt{2}$-2 | B. | 3$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
5.计算(-3)m+2×(-3)m-1,得( )
| A. | 3m-1 | B. | (-3)m-1 | C. | -(-3)m-1 | D. | (-3)m |
19.计算(6×103)•(8×105)的结果是( )
| A. | 48×109 | B. | 48×1015 | C. | 4.8×108 | D. | 4.8×109 |
 如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相较于点M,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.
如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相较于点M,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C. 如图,△ABC是等腰直角三角板,∠C=90°,AC=BC=6,将含30°角的三角板GMF的直角顶点与△ABC斜边AB的中点M重合,当三角板GMF的直角顶点绕着点M旋转时,两直角边始终保持分别与边AC、BC交于D、E两点(D、E不与A、B重合)
如图,△ABC是等腰直角三角板,∠C=90°,AC=BC=6,将含30°角的三角板GMF的直角顶点与△ABC斜边AB的中点M重合,当三角板GMF的直角顶点绕着点M旋转时,两直角边始终保持分别与边AC、BC交于D、E两点(D、E不与A、B重合)