题目内容
爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )
A. 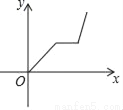 B.
B. 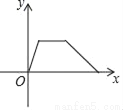 C.
C. 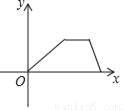 D.
D. 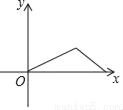
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
题目内容
爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案