题目内容
20.已知:$\sqrt{x-y+3}$与$\sqrt{x+2y}$互为相反数,求(x+y)2016的平方根.分析 根据相反数的性质列出算式,根据非负数的性质列出二元一次方程组,解方程组求出x、y的值,根据平方根的概念解答即可.
解答 解:由已知可得:$\sqrt{x-y+3}$+$\sqrt{x+2y}$=0,
则$\left\{\begin{array}{l}{x-y+3=0}\\{x+2y=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$,
∴(x+y)2016=1,
∴(x+y)2016的平方根是±1.
点评 本题考查的是非负数的性质、二元一次方程组的解法,掌握非负数之和等于0时,各项都等于0是解题的关键.

练习册系列答案
相关题目
8. 小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
 小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )| A. | 各项消费金额占消费总金额的百分比 | |
| B. | 各项消费的金额 | |
| C. | 各项消费金额的增减变化情况 | |
| D. | 消费的总金额 |
9.下列说法正确的是( )
| A. | x2-x=0是二项方程 | B. | $\frac{x-1}{2}-\frac{x}{3}=4$是分式方程 | ||
| C. | $\sqrt{2}{x^2}-2x=\sqrt{3}$是无理方程 | D. | 2x2-y=4是二元二次方程 |
10.已知x>y,则下列不等式成立的是( )
| A. | x-1<y-1 | B. | 3x<3y | C. | -x<-y | D. | $\frac{x}{2}<\frac{y}{2}$ |
 (1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.
(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.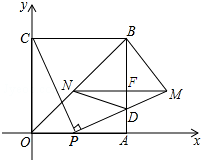 如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥AO,交BO于点N,连结ND、BM,设OP=t.
如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥AO,交BO于点N,连结ND、BM,设OP=t.