题目内容
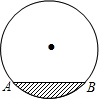 维修人员为更换一圆柱形的输水管道,需先确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面,若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
维修人员为更换一圆柱形的输水管道,需先确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面,若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.考点:垂径定理的应用,勾股定理
专题:
分析:连接OA,作半径OE⊥AB 于点D,设圆的半径为xcm,则OD=(x-4)cm,在Rt△AOD中,根据勾股定理即可得出x的值即可得出结论.
解答: 解:连接OA,作半径OE⊥AB于点D,设圆的半径为xcm,则OD=(x-4)cm,
解:连接OA,作半径OE⊥AB于点D,设圆的半径为xcm,则OD=(x-4)cm,
∵OE⊥AB,
∴AD=BD=16÷2=8 (cm),
在Rt△AOD中,OA2-OD2=AD2,即x2-(x-4)2=82,
解得x=10.
答:圆的半径为10cm.
 解:连接OA,作半径OE⊥AB于点D,设圆的半径为xcm,则OD=(x-4)cm,
解:连接OA,作半径OE⊥AB于点D,设圆的半径为xcm,则OD=(x-4)cm,∵OE⊥AB,
∴AD=BD=16÷2=8 (cm),
在Rt△AOD中,OA2-OD2=AD2,即x2-(x-4)2=82,
解得x=10.
答:圆的半径为10cm.
点评:本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目

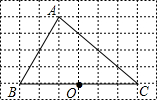 如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.
如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点. 如图,A、D是直线l1上两点,B、C是直线l2上两点,且AB⊥BC,CD⊥AD.
如图,A、D是直线l1上两点,B、C是直线l2上两点,且AB⊥BC,CD⊥AD. 如图,点D,E分别在△ABC的边AB,AC上,且AB=9,AC=6,AD=3,AE=
如图,点D,E分别在△ABC的边AB,AC上,且AB=9,AC=6,AD=3,AE=