题目内容
17．下列因式分解正确的是（ ）| A． | 4a2-4a+1=4a（a-1）+1 | B． | x2-4y2=（x+4y）（x-4y） | ||
| C． | $\frac{9}{4}$x2-x+$\frac{1}{9}$=（$\frac{3}{2}$x-$\frac{1}{3}$）2 | D． | 2xy-x2-y2=-（x+y）2 |
分析 直接利用完全平方公式分解因式进而判断得出答案．
解答 解：A、4a2-4a+1=4a（a-1）+1，不是因式分解，故此选项错误；
B、x2-4y2=（x+2y）（x-2y），故此选项错误；
C、$\frac{9}{4}$x2-x+$\frac{1}{9}$=（$\frac{3}{2}$x-$\frac{1}{3}$）2，正确；
D、2xy-x2-y2=-（x-y）2，故此选项错误；
故选：C．
点评 此题主要考查了公式法因式分解，正确应用完全平方公式是解题关键．
练习册系列答案
相关题目
5．在△ABC中，A，B都是锐角，且sinA=$\frac{\sqrt{3}}{2}$，tanB=$\sqrt{3}$，AB=8，则AB边上的高为（ ）
| A． | 4$\sqrt{3}$ | B． | 8$\sqrt{3}$ | C． | 16$\sqrt{3}$ | D． | 24$\sqrt{3}$ |
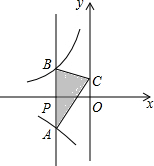如图，过x轴负半轴上的任意一点P，作y轴的平行线，分别与反比例函数y=$\frac{-6}{x}$，y=$\frac{4}{x}$交于A，B两点．若点C是y轴上任意一点，连接AC，BC，则△ABC的面积是5．
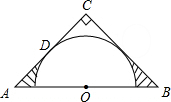如图，在△ABC中，∠C=90°，AC=BC，AB=2$\sqrt{2}$，点O为AB的中点，以点O为圆心作半圆与边AC相切于点D．则图中阴影部分的面积为1-$\frac{π}{4}$．
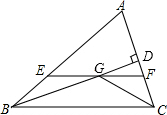如图，在△ABC中，∠ABC和∠ACB的平分线相交于点G，过点G作EF∥BC交AB于E，交AC于F，过点G作GD⊥AC于D，下列四个结论：