题目内容
 如图,?ABCD中,AE:EB=1:2,则△AEF与△CDF的周长比为
如图,?ABCD中,AE:EB=1:2,则△AEF与△CDF的周长比为考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:根据ABCD是平行四边形,推出△AEF∽△CDF,利用△AEF与△CDF周长的比等于相似比即可求得.再利用△AEF与△CDF周长的比等于相似比为1:3.由相似三角形面积比是相似比的平方,即可求得答案.
解答:解:由AE:EB=1:2,
得
=
,
又∵四边形ABCD是平行四边形,
∴△AEF∽△CDF,
由AB=CD得
=
,
∴△AEF与△CDF周长的比等于相似比等于1:3.
由
=
,(相似三角形面积比是相似比的平方)
由S△AEF=6cm2,
解得S△CDF=54cm2.
得
| AE |
| AB |
| 1 |
| 3 |
又∵四边形ABCD是平行四边形,
∴△AEF∽△CDF,
由AB=CD得
| AE |
| CD |
| 1 |
| 3 |
∴△AEF与△CDF周长的比等于相似比等于1:3.
由
| S△AEF |
| S△CDF |
| 1 |
| 9 |
由S△AEF=6cm2,
解得S△CDF=54cm2.
点评:此题考查学生对相似三角形的判定与性质、三角形的面积、平行四边形的性质等知识点的理解与掌握.此题主要利用了相似三角形周长比等于相似比和相似三角形面积比是相似比的平方.

练习册系列答案
相关题目
(
-3
+2
)×
的值是( )
| 24 |
| 15 |
2
|
| 2 |
A、
| ||||||
B、3
| ||||||
C、2
| ||||||
D、
|

 若在图中三顶点以外之18个圆圈内填入适当的数,使得任何一线段上相邻三个数均成等差,则位置A所填的数为
若在图中三顶点以外之18个圆圈内填入适当的数,使得任何一线段上相邻三个数均成等差,则位置A所填的数为 如图,反比例函数
如图,反比例函数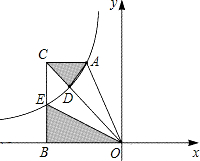 如图,在平面直角坐标系中,直角梯形AOBC的边OB在x轴的负半轴上,AC∥OB,∠OBC=90°,过A点的双曲线y=
如图,在平面直角坐标系中,直角梯形AOBC的边OB在x轴的负半轴上,AC∥OB,∠OBC=90°,过A点的双曲线y=