题目内容
12.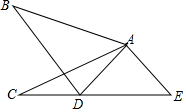 如图,在△ABD和△ACE中,有下列论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中三个论断作为条件,另一个论断作为结论,写出一个真命题:如果AB=AC,AD=AE,BD=CE,那么∠B=∠C.
如图,在△ABD和△ACE中,有下列论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中三个论断作为条件,另一个论断作为结论,写出一个真命题:如果AB=AC,AD=AE,BD=CE,那么∠B=∠C.
分析 命题为:如果AB=AC,AD=AE,BD=CE,那么∠B=∠C,根据SSS推出两三角形全等,根据全等三角形的性质得出即可.
解答 解:命题为:如果AB=AC,AD=AE,BD=CE,那么∠B=∠C,
理由是:∵在△ABD和△ACE中
$\left\{\begin{array}{l}{AD=AE}\\{AB=AC}\\{BD=CE}\end{array}\right.$
∴△ABD≌△ACE(SSS),
∴∠B=∠C,
故答案为:如果AB=AC,AD=AE,BD=CE,那么∠B=∠C.
点评 本题考查了全等三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列各组条件中,能确定△ABC≌△DEF的是( )
| A. | ∠A=∠D,∠B=∠E,∠C=∠F | B. | ∠A=∠D,∠C=∠F,AC=DF | ||
| C. | ∠A=∠D,∠C=∠F,AC=EF | D. | AB=DE,BC=EF,∠A=∠D |
1.若a-b=1,ab=4,则下列代数式a3b-2a2b2+ab3的值( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
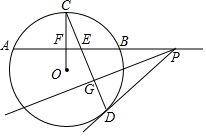 如图,在⊙O中,OC⊥AB于点F,弦CD交弦AB于点E,线段ED的垂直平分线GP交AB延长线于点P,连结PD.
如图,在⊙O中,OC⊥AB于点F,弦CD交弦AB于点E,线段ED的垂直平分线GP交AB延长线于点P,连结PD.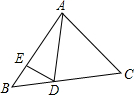 如图,△ABC中,D、E分别是BC、AB边上的点,AD平分∠EDC,试说明∠BED>∠B的道理.
如图,△ABC中,D、E分别是BC、AB边上的点,AD平分∠EDC,试说明∠BED>∠B的道理.