题目内容
7.已知α,β是方程x2+2x+m=0的两个根,且a2+3a+β>0,求m的取值范围.分析 根据根的判别式和一元二次方程根与系数的关系解答.
解答 解:∵α,β是方程x2+2x+m=0的两个根,
∴△≥0,
∴4-4m≥0,解得m≤1;
∵a2+3a+β>0,
∴a2+2a+α+β>0,
∴-m-2>0,
∴m<-2;
综上所述,m<-2.
点评 本题考查了根的判别式和一元二次方程根与系数的关系,要知道一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系为:x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
18.压路机前轮转动一周,求压过的面积是多少,这是求圆柱的( )
| A. | 侧面积 | B. | 表面积 | C. | 体积 |
15.我校准备在初二年级的四名同学中选拔一名参加我市“风采小主持人”大赛,选拔赛中每名学生的平均成绩及方差如表所示,若要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均成绩 | 8 | 9 | 9 | 8 |
| 方差 | 1 | 1 | 1.2 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
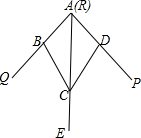 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( ) 如图,将Rt△ABC放置在平面直角坐标系中,C与原点重合,CB在x轴上,若AB=2,点B的坐标为(4,0),则点A的坐标为(3,$\sqrt{3}$).
如图,将Rt△ABC放置在平面直角坐标系中,C与原点重合,CB在x轴上,若AB=2,点B的坐标为(4,0),则点A的坐标为(3,$\sqrt{3}$).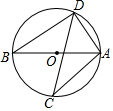 如图,AB为⊙O的直径,CD是⊙O的弦,∠ACD=25°,则∠BAD=65°.
如图,AB为⊙O的直径,CD是⊙O的弦,∠ACD=25°,则∠BAD=65°.