题目内容
16.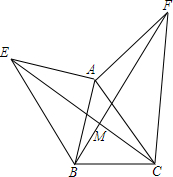 如图所示,已知△BAE和△CAF为等腰直角三角形.求证:
如图所示,已知△BAE和△CAF为等腰直角三角形.求证:(1)EC=BF;
(2)EC⊥BF.
分析 (1)要证EC=BF可转化为证明△EAC≌△BAF,由已知可证AB=AE,AC=AF,∠BAE=∠CAF=90°,因为∠BAE+∠BAC=∠CAF+∠BAC,即可证∠EAC=∠BAF,符合SAS,即得证;
(2)由三角形求得得出∠AFB=∠ACE,然后根据三角形内角和定理和等量代换得出∠BMC=∠BAC+∠ABF+∠AFB,然后根据∠BAC+∠CAF+∠ABF+∠AFB=180°,∠CAF=90°,即可证得结论.
解答 证明:(1)∵△BAE和△CAF为等腰直角三角形.
∴AB=AE,AC=AF,∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
即∠EAC=∠BAF,
在△EAC与△BAF中,
$\left\{\begin{array}{l}{AE=AB}\\{∥EAC=∠BAF}\\{AC=AF}\end{array}\right.$,
∴△EAC≌△BAF(SAS),
∴EC=BF;
(2)∵△EAC≌△BAF,
∴∠AFB=∠ACE,
∵∠BMC=180°-(∠MBC+∠MCB)=180°-(∠ABC-∠ABF+∠ACB-∠ACE)=180°-(180°-∠BAC-∠ABF-∠AFB)=∠BAC+∠ABF+∠AFB,
∵∠BAC+∠CAF+∠ABF+∠AFB=180°,∠CAF=90°,
∴∠BAC+∠ABF+∠AFB=90°,
∴∠BMC=90°,
∴EC⊥BF.
点评 本题考查了等腰直角三角形的性质,三角形全等的判定和性质,三角形内角和定理,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
4.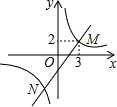 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )| A. | 2,2 | B. | 3,8 | C. | 2,6 | D. | -2,-8 |
8.在下列常见的手机软件小图标中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.解决下列问题,比较容易用普查方式的是( )
| A. | 了解菏泽市中小学生近视率 | B. | 了解菏泽市初中生体育中考的成绩 | ||
| C. | 了解菏泽居民的人均收入情况 | D. | 了解某一天离开菏泽市的人口数量 |
6.$\frac{1}{5}$x2+0.7=2.5的根是( )
| A. | x=3 | B. | x=±3 | C. | x=±9 | D. | x=±$\sqrt{3}$ |
 已知:如图,直线AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,
已知:如图,直线AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,