题目内容
4.根据条件求二次函数的解析式(1)二次函数y=ax2+bx+c的对称轴为x=3,最小值为-2,且过(0,1)点.
(2)抛物线过(-1,0),(3,0),(1,-5)三点.
分析 (1)设顶点式为y=a(x-3)2-2,然后把(0,1)代入求出a即可;
(2)设交点式为y=a(x+1)(x-3),然后把(1,-5)代入求出a即可.
解答 解:(1)设抛物线解析式为y=a(x-3)2-2,
把(0,1)代入得9a-2=1,解得a=$\frac{1}{3}$,
所以抛物线解析式为y=$\frac{1}{3}$(x-3)2-2;
(2)设抛物线解析式为y=a(x+1)(x-3),
把(1,-5)代入得a•2•(-2)=-5,解得a=$\frac{5}{4}$,
所以抛物线解析式为y=$\frac{5}{4}$(x+1)(x-3),
即y=$\frac{5}{4}$x2-$\frac{5}{2}$x-$\frac{15}{4}$.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
19.若x1,x2是方程x2-6x+10=0的两根,则x1+x2的值是( )
| A. | 10 | B. | 6 | C. | -6 | D. | 以上都不对 |
13.下列式子不是无理数的是( )
| A. | $\frac{π}{6}$ | B. | π+5 | C. | (π-2011)0 | D. | π-3.14 |
 如图,在△ABC中,DE∥FG∥BC,AD:DF:FB=3:2:1,则△ADE、四边形DFGE、四边形FBCG的面积比为9:16:11.
如图,在△ABC中,DE∥FG∥BC,AD:DF:FB=3:2:1,则△ADE、四边形DFGE、四边形FBCG的面积比为9:16:11.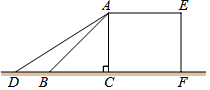 如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601,$\sqrt{2}$≈1.414].
如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601,$\sqrt{2}$≈1.414].