题目内容
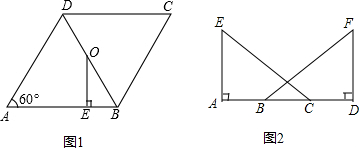
(1)如图1,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
①求∠ABD 的度数; ②求线段BE的长.
(2)已知:如图2,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.
求证:∠ACE=∠DBF.
①求∠ABD 的度数; ②求线段BE的长.
(2)已知:如图2,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.
求证:∠ACE=∠DBF.

考点:菱形的性质,全等三角形的判定与性质
专题:
分析:(1)①证明△ABD为等边三角形,即可解决问题;
②求出BO的长度,运用直角三角形的边角关系即可解决问题.
(2)证明△AEC≌△DFB,即可解决问题.
②求出BO的长度,运用直角三角形的边角关系即可解决问题.
(2)证明△AEC≌△DFB,即可解决问题.
解答: 解:(1)①如图1,∵四边形ABCD为菱形,
解:(1)①如图1,∵四边形ABCD为菱形,
∴AB=AD;而∠A=60°,AB=4,
∴△ABD为等边三角形,且BD=AB=4;
∵△ABD为等边三角形,
∴∠ABD=60°.
②∵O为对角线BD的中点,
∴BO=DO=2;
∵OE⊥AB,∠EBO=90°,
∴sin60°=
,OE=
,BE=1.
(2)如图2,
∵AB=DC,
∴AC=BD;而EA⊥AD,FD⊥AD,
∴∠A=∠D;
在△AEC与△DFB中,
,
∴△AEC≌△DFB(SAS),
∴∠ACE=∠DBF.
 解:(1)①如图1,∵四边形ABCD为菱形,
解:(1)①如图1,∵四边形ABCD为菱形,∴AB=AD;而∠A=60°,AB=4,
∴△ABD为等边三角形,且BD=AB=4;
∵△ABD为等边三角形,
∴∠ABD=60°.
②∵O为对角线BD的中点,
∴BO=DO=2;
∵OE⊥AB,∠EBO=90°,
∴sin60°=
| OE |
| OB |
| 3 |
(2)如图2,
∵AB=DC,
∴AC=BD;而EA⊥AD,FD⊥AD,
∴∠A=∠D;
在△AEC与△DFB中,
|
∴△AEC≌△DFB(SAS),
∴∠ACE=∠DBF.
点评:该题主要考查了菱形的性质、全等三角形的判定及其性质的应用等几何知识点问题;牢固掌握全等三角形的判定、菱形的性质是关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若|x+y+2|+(xy-1)2=0,则(3x-xy+1)-(xy-3y-2)的值为( )
| A、3 | B、-3 | C、-5 | D、11 |
 如图,AE∥DC,∠A=∠C,BD平分∠ADC,则下列说法不正确的是( )
如图,AE∥DC,∠A=∠C,BD平分∠ADC,则下列说法不正确的是( )| A、AD∥BC |
| B、BC=DC |
| C、F为E中点 |
| D、AF=AD |
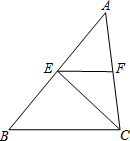 如图,在△ABC中,E、F分别是AB、AC的中点,△CEF的面积为2.5,则△ABC的面积为
如图,在△ABC中,E、F分别是AB、AC的中点,△CEF的面积为2.5,则△ABC的面积为
 如图,在△ABC中,分别以点A和点B为圆心,大于
如图,在△ABC中,分别以点A和点B为圆心,大于 如图,直线AB,CD相交于点O,OE分∠AOD成两个角,∠AOE:∠EOD=2:6,∠BOD-∠BOC=20°,求∠AOE的度数.
如图,直线AB,CD相交于点O,OE分∠AOD成两个角,∠AOE:∠EOD=2:6,∠BOD-∠BOC=20°,求∠AOE的度数. 用“>”或“<”号填空:有理数a,b,c在数轴上对应的点如图:
用“>”或“<”号填空:有理数a,b,c在数轴上对应的点如图: