题目内容
12.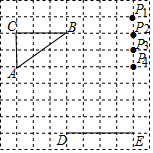 如图,在方格纸中,△ABC和△DPE的顶点均在格点上,要使△ABC∽△DPE,则点P所在的格点为( )
如图,在方格纸中,△ABC和△DPE的顶点均在格点上,要使△ABC∽△DPE,则点P所在的格点为( )| A. | P1 | B. | P2 | C. | P3 | D. | P4 |
分析 利用两个三角形都为直角三角形,则根据两组对应边的比相等且夹角对应相等的两个三角形相似,当$\frac{PE}{BC}$=$\frac{DE}{AC}$时,△ABC∽△DPE,然后利用比例性质计算出PE后可判断P点的位置.
解答 解:∵∠DEP=∠ACB,
∴当$\frac{PE}{BC}$=$\frac{DE}{AC}$时,△ABC∽△DPE,
即$\frac{PE}{3}$=$\frac{4}{2}$,
∴PE=6,
∴点P在格点P2的位置.
故选B.
点评 本题考查了相似三角形的判定:根据已知条件合理使用相似三角形的判定方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学记数法表示是( )
| A. | 0.95×1013km | B. | 950×1010km | C. | 95×1011km | D. | 9.5×1012km |
4.下列关于点和线的说法中,正确的是( )
| A. | 线段比直线长 | |
| B. | 过同一平面内的两点,可以作三条直线 | |
| C. | 一条射线有两个端点 | |
| D. | 两点之间的所有连线中,线段最短 |
 如图所示,平面直角坐标系中,△ABC的边AB在x轴上,∠C=60°,AC交y轴于点E,AC,BC的长是方程x2-16x+64=0的两个根且OA:OB=1:3,请解答下列问题:
如图所示,平面直角坐标系中,△ABC的边AB在x轴上,∠C=60°,AC交y轴于点E,AC,BC的长是方程x2-16x+64=0的两个根且OA:OB=1:3,请解答下列问题: 体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.