Question

9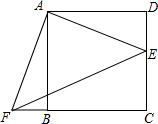．如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转至△ABF的位置．
（1）旋转中心是点A，旋转角度是90度；
（2）若连结EF，则△AEF是等腰直角三角形；并证明；
（3）若四边形AECF的面积为36，DE=2，求EF的长．

Answer 1

分析 （1）根据题意，即可确定旋转中心，旋转角．
（2）结论：△AEF是等腰直三角形．：由△ABF≌△ADE，推出AF=AE，∠FAB=∠DAE，推出∠FAE=∠DAB=90°即可证明．
（3）理由（2）的结论EF=$\sqrt{2}$AE，求出AE即可解决问题．

解答 解：（1）由题意旋转中心为点A，旋转角为90°；  
故答案为A，90．

（2）结论：△AEF是等腰直三角形．
理由：∵△ABF≌△ADE，
∴AF=AE，∠FAB=∠DAE，
∴∠FAE=∠DAB=90°．
∴△AEF是等腰直角三角形，
故答案为等腰直角．

（3）∵正方形ABCD的面积为36，
∴AD=BC=CD=AB=6，
在Rt△ADE中，∵AD=6，DE=2，
∴AE=AF=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$，
∵△AEF是等腰直角三角形，
∴EF=$\sqrt{2}$AE=4$\sqrt{5}$．

点评 本题考查旋转的性质、正方形的性质、等腰直角三角形的性质、勾股定理等知识，解题的关键是利用旋转不变性解决问题，属于中考常考题型．