题目内容
14.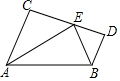 如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD(要求:用两种方法证明):
如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD(要求:用两种方法证明):①用割的方法;
②用补的方法.
分析 ①如图(1)在AB上截取AF=AC,连结EF,可证明△ACE≌△AFE,进一步可证明△EFB≌△EDB,再利用全等三角形的性质结合线段的和差可证明结论;
②如图(2),延长BE,与AC的延长线相交于点F,可证明△AEF≌△AEB,进一步可证明△BED≌△FEC,再利用全等三角形的性质结合线段的和差可证明结论.
解答 证明:
①如图(1)在AB上截取AF=AC,连结EF,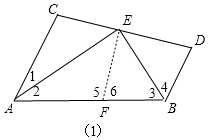
在△ACE和△AFE中,
$\left\{\begin{array}{l}{AC=AF}\\{∠1=∠2}\\{AE=AE}\end{array}\right.$
∴△ACE≌△AFE(SAS),
∴∠5=∠C,
∴AC∥BD,
∴∠C+∠D=180°,
∵∠5+∠6=180°,
∴∠6=∠D,
在△EFB和△BDE中,
$\left\{\begin{array}{l}{∠6=∠D}\\{∠3=∠4}\\{BE=BE}\end{array}\right.$
∴△EFB≌△EDB(AAS),
∴FB=DB,
∴AC+BD=AF+FB=AB;
②如图(2),延长BE,与AC的延长线相交于点F,
∵AC∥BD,
∴∠F=∠4,
∵∠3=∠4,
∴∠F=∠3
在△AEF和△AEB中
$\left\{\begin{array}{l}{∠F=∠3}\\{∠1=∠2}\\{AE=AE}\end{array}\right.$,
∴△AEF≌△AEB(AAS),
∴AB=AF,BE=FE,
在△BED和△FEC中,
$\left\{\begin{array}{l}{∠5=∠6}\\{BE=FE}\\{∠4=∠F}\end{array}\right.$,
∴△BED≌△FEC(ASA),
∴BD=FC,
∴AB=AF=AC+CF=AC+BD.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应角相等、对应边相等)是解题的关键.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -2 | -4 | +12 | -10 | +16 | -8 |
(2)产量最多的一天比产量最少的一天多生产自行车26辆;
(4)该厂实行每周计件工资制,每生产一辆车可得30元,若超额完成任务,则超过部分每辆另奖20元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少元?
 如图,一根旗杆在一次强台风中被吹断,倒下部分与地面成30°角,触地点到旗杆底部的距离BC=6m,求这根旗杆折断前的高度.(答案保留根号)
如图,一根旗杆在一次强台风中被吹断,倒下部分与地面成30°角,触地点到旗杆底部的距离BC=6m,求这根旗杆折断前的高度.(答案保留根号)
 在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=6,AB=10.求△ABD的面积.
在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=6,AB=10.求△ABD的面积.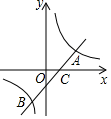 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).