题目内容
4．
如图，一根旗杆在一次强台风中被吹断，倒下部分与地面成30°角，触地点到旗杆底部的距离BC=6m，求这根旗杆折断前的高度．（答案保留根号）
分析 根据题意可以得直角三角形中，较短的直角边是5，再根据30°所对的直角边是斜边的一半，得斜边是10，从而求出大树的高度．
解答 解：如图，在Rt△ABC中，∠C=90°，CB=6，∠A=30°，
则AC=2$\sqrt{3}$m，AB=4$\sqrt{3}$m，
则大树的高度为2$\sqrt{3}$+4$\sqrt{3}$=6$\sqrt{3}$m．
故这根旗杆折断前的高度是6$\sqrt{3}$m．
点评 此题考查了勾股定理的应用，此题要求学生主要掌握直角三角形的性质：30°所对的直角边是斜边的一半．
练习册系列答案
相关题目
14．观察下列等式：a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$，a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$，a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$，a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$，…，按以上规律写出了a5、a6、a7、…、a20，则a1+a2+a3+…+a20=（ ）
| A． | $\frac{1}{2}$-$\frac{1}{20×{2}^{20}}$ | B． | $\frac{1}{19×{2}^{19}}$-$\frac{1}{20×{2}^{20}}$ | ||
| C． | $\frac{1}{20}$-$\frac{1}{21×{2}^{21}}$ | D． | $\frac{1}{2}$-$\frac{1}{21×{2}^{21}}$ |
19．
如图，直线y=kx+b经过一、二、四象限，若P（x1，y1），Q（x2，y2）是该直线上两个不同的点，且x1＞x2，则y1-y2的值（ ）
如图，直线y=kx+b经过一、二、四象限，若P（x1，y1），Q（x2，y2）是该直线上两个不同的点，且x1＞x2，则y1-y2的值（ ）| A． | 大于0 | B． | 大于等于0 | C． | 等于0 | D． | 小于0 |
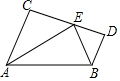如图，已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，求证：AB=AC+BD（要求：用两种方法证明）：