��Ŀ����
8��������Ȫ��ͼ1������ʹ��ˮ���������ֵĽ�������仯���仯��ij��������Ȫ��״�������ߣ������ˮ��Ϊԭ�㣬��ˮ���밶��18m�����ֱ仯ʱ�������ߵĶ�����ֱ��y=kx�ϱ䶯���Ӷ�����һ�鲻ͬ�������ߣ�ͼ2�������������ߵ�ͳһ��ʽΪy=ax2+bx����1������֪k=1���������������ˮ�����߶ȴ�3m�����ʱa��b��ֵ��
��2����k=1�������ˮǡ�ôﵽ���ߣ����ʱ�����������ˮ�����߶��Ƕ����ף�
��3����k=2����Ҫ�������������ˮ�߲��ܵ����ߣ���a��ȡֵ��Χ��
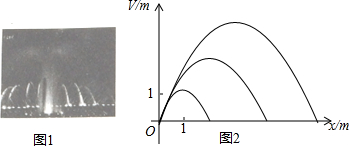
���� ��1�����������ߵĶ�����ֱ��y=kx�ϣ�������Ϊy=ax2+bx��k=1���������������ˮ�����߶ȴ�3m���������a��b��ֵ��
��2������k=1�������ˮǡ�ôﵽ���ߣ������ߵĶ�����ֱ��y=kx�ϣ�������������ߵĶԳ���x��ֵ���Ӷ����Եõ���ʱ�����������ˮ�����߶ȣ�
��3�������ߵĶ�����ֱ��y=2x�Ͽɵ�b��ֵ�����������������ˮ�߲��ܵ����ߣ�����ˮ���밶��18m��֪��Գ���-$\frac{b}{2a}$��9���ɵ�a�ķ�Χ��
��� �⣺��1����y=ax2+bx�Ķ���Ϊ��-$\frac{b}{2a}$��-$\frac{{b}^{2}}{4a}$���������ߵĶ�����ֱ��y=kx�ϣ�k=1��������ˮ�����߶ȴ�3m��
��-$\frac{b}{2a}$=$\frac{-{b}^{2}}{4a}$��$\frac{-{b}^{2}}{4a}$=3��
��ã�a=-$\frac{1}{3}$��b=2��
��k=1���������������ˮ�����߶ȴ�3m����ʱa��b��ֵ�ֱ���-$\frac{1}{3}$��2��
��2����k=1�������ˮǡ�ôﵽ���ߣ���ˮ���밶��18m�������ߵĶ�����ֱ��y=kx�ϣ�
���ʱ�����ߵĶԳ���Ϊx=9��y=x=9��
����ʱ�����������ˮ�����߶���9�ף�
��3����y=ax2+bx�Ķ���Ϊ��-$\frac{b}{2a}$��-$\frac{{b}^{2}}{4a}$���������ߵĶ�����ֱ��y=2x�ϣ�
��-$\frac{b}{2a}$��2=-$\frac{-{b}^{2}}{4a}$��
��ã�b=4��
�������������ˮ�߲��ܵ����ߣ���ˮ���밶��18m��
��-$\frac{b}{2a}$��9������-$\frac{4}{2a}$��9��
��ã�a��-$\frac{2}{9}$��
���� ���⿼����κ�����Ӧ�ã�����Ĺؼ�����ȷ���⣬������Ŀ��������Ϣ�г���Ӧ�Ĺ�ϵʽ���ҳ�����������Ҫ��������

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�| A�� | 25% | B�� | 30% | C�� | 15% | D�� | 20% |
| x | �� | 0 | 1 | 2 | 3 | 4 | �� |
| y | �� | 3 | 0 | -1 | 0 | 3 | �� |
��2����������y=x2+bx+c��������ƽ�ƣ�ʹ���Ķ���Ϊ����ԭ�㣿
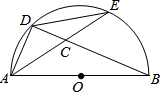 ��ͼ��ʾ��AB�ǡ�O��ֱ����D��E�ǰ�Բ���������㣬����AD��DE��AE��BD�ཻ�ڵ�C��Ҫ�ǡ�ADC���ABD���ƣ���������һ���������������ӵ������д�����ǣ�������
��ͼ��ʾ��AB�ǡ�O��ֱ����D��E�ǰ�Բ���������㣬����AD��DE��AE��BD�ཻ�ڵ�C��Ҫ�ǡ�ADC���ABD���ƣ���������һ���������������ӵ������д�����ǣ�������| A�� | ��ACD=��DAB | B�� | AD=DE | C�� | AD•AB=CD•BD | D�� | AD2=BD•CD |
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | ������� |
| A�� | m��1 | B�� | m��1 | C�� | m��1��m��0 | D�� | m��1��m��0 |