题目内容
9.设[x]表示不大于x的最大整数,例如[-2.1]=-3,[3.2]=3;则满足x2=-2x[x]+4,与-2<x<2的实数x为-1+$\sqrt{5}$.分析 分①-2<x<-1,②-1≤x<0,③0≤x<1,④1≤x<2四种情况,得到关于x的一元二次方程,解方程即可求解.注意要考虑x的取值范围.
解答 解:x2=-2x[x]+4,
①-2<x<-1,x2=4x+4,解得x=2±2$\sqrt{2}$(不合题意舍去);
②-1≤x<0,x2=2x+4,解得x=1±$\sqrt{5}$(不合题意舍去);
③0≤x<1,x2=4,解得x=±2(不合题意舍去);
④1≤x<2,x2=-2x+4,解得x=-1-$\sqrt{5}$(不合题意舍去)或x=-1+$\sqrt{5}$.
故满足x2=-2x[x]+4,与-2<x<2的实数x为-1+$\sqrt{5}$.
故答案为:-1+$\sqrt{5}$.
点评 考查了取整计算,要了解取整函数的定义,注意分类思想的应用.

练习册系列答案
相关题目
9.下列一元二次方程两实数根和为4的是( )
| A. | x2+2x-4=0 | B. | x2+2x+10=0 | C. | x2-4x+4=0 | D. | x2+4x-5=0 |
 在平行四边形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,求证:EF⊥AE.
在平行四边形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,求证:EF⊥AE. 已知方程组$\left\{\begin{array}{l}{ax-3y=5}\\{2x-by=1}\end{array}\right.$所对应的图象如图所示,试求出3a+7b的值.
已知方程组$\left\{\begin{array}{l}{ax-3y=5}\\{2x-by=1}\end{array}\right.$所对应的图象如图所示,试求出3a+7b的值.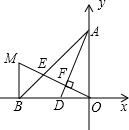 如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.
如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.