Question

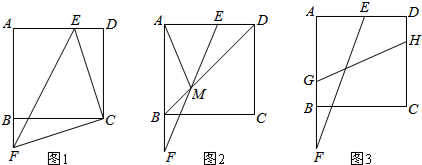
19．如图1，正方形ABCD的边长为6cm，点F从点B出发，沿射线AB方向以1cm/秒的速度移动，点E从点D出发，向点A以1cm/秒的速度移动（不到点A）．设点E，F同时出发移动t秒．
（1）在点E，F移动过程中，连接CE，CF，EF，则△CEF的形状是等腰直角三角形，始终保持不变；
（2）如图2，连接EF，设EF交BD移动M，当t=2时，求AM的长；
（3）如图3，点G，H分别在边AB，CD上，且GH=3$\sqrt{5}$cm，连接EF，当EF与GH的夹角为45°，求t的值．

Answer 1

分析 （1）通过证明△CDE≌△CBF得到CF=CE，∠DCE=∠BCF，则易推知△CEF是等腰直角三角形；
（2）过点E作EN∥AB，交BD于点N，∠END=∠ABD=∠EDN=45°，EN=ED=BF．可证△EMN≌△FMB，则其对应边相等：EM=FM．所以在Rt△AEF中，由勾股定理求得EF的长度，则AM=$\frac{1}{2}$EF；
（3）如图3，连接CE，CF，设EF与GH交于P．购进平行四边形GFCH，则其对边相等：CF=GH=3$\sqrt{5}$．所以在Rt△CBF中，由勾股定理得到：BF=$\sqrt{C{F}^{2}-B{C}^{2}}$=3，故t=3．

解答 解：（1）等腰直角三角形．理由如下：
如图1，在正方形ABCD中，DC=BC，∠D=∠ABC=90°．
依题意得：DE=BF=t．
在△CDE与△CBF中，
$\left\{\begin{array}{l}{DC=BC}\\{∠D=∠CBF}\\{DE=BF}\end{array}\right.$，
∴△CDE≌△CBF（SAS），
∴CF=CE，∠DCE=∠BCF，
∴∠ECF=∠BCF+∠BCE=∠DCE+∠BCE=∠BCD=90°，
∴△CEF是等腰直角三角形．
故答案是：等腰直角三角形．

（2）如图2，过点E作EN∥AB，交BD于点N，则∠NEM=∠BFM．
∴∠END=∠ABD=∠EDN=45°，
∴EN=ED=BF．
在△EMN与△FMB中，
$\left\{\begin{array}{l}{∠NME=∠BMF}\\{∠NEM=∠BFM}\\{EN=BF}\end{array}\right.$，
∴△EMN≌△FMB（AAS），
∴EM=FM．
∵Rt△AEF中，AE=4，AF=8，
∴$\sqrt{A{E}^{2}+A{F}^{2}}$=EF=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$，
∴AM=$\frac{1}{2}$EF=2$\sqrt{5}$；

（3）如图3，连接CE，CF，设EF与GH交于P．
由（1）得∠CFE=45°，又∠EPQ=45°，
∴GH∥CF，
又∵AF∥DC，
∴四边形GFCH是平行四边形，
∴CF=GH=3$\sqrt{5}$，
在Rt△CBF中，得BF=$\sqrt{C{F}^{2}-B{C}^{2}}$=$\sqrt{45-36}$=3，
∴t=3．

点评 本题考查了四边形综合题．解题过程中，涉及到了平行四边形的判定与性质，全等三角形的判定与性质以及勾股定理的应用．解答该类题目时，要巧妙的作出辅助线，构建几何模型，利用特殊的四边形的性质（或者全等三角形的性质）得到相关线段间的数量关系，从而解决问题．