题目内容
在平面直角坐标系中,B(1,0)、A(3,-3)、C(3,0),点P在y轴的正半轴上运动,若以O、B、P为顶点的三角形与△ABC相似,则点P的坐标为 .
考点:相似三角形的判定,坐标与图形性质
专题:计算题
分析:利用点A、B、C的坐标特征得到∠ACB=90°,CB=2,CA=3,设P点坐标为(0,t),由于∠POB=∠ACB,根据两组对应边的比相等且夹角对应相等的两个三角形相似,当
=
时,△OPB∽△CBA,即
=
或当
=
时,△OPB∽△CAB,即
=
,然后分别求出t的值,从而得到P点坐标.
| OP |
| BC |
| OB |
| CA |
| |t| |
| 2 |
| 1 |
| 3 |
| OP |
| CA |
| OB |
| CB |
| |t| |
| 3 |
| 1 |
| 2 |
解答:解: ∵B(1,0)、A(3,-3)、C(3,0),
∵B(1,0)、A(3,-3)、C(3,0),
∴∠ACB=90°,CB=2,CA=3,
设P点坐标为(0,t),
∵∠POB=∠ACB=90°,
∴当
=
时,△OPB∽△CBA,即
=
,解得t=±
,此时P点坐标为(0,
)或(0,-
);
当
=
时,△OPB∽△CAB,即
=
,解得t=±
,此时P点坐标为(0,
)或(0,-
),
综上所述,若以O、B、P为顶点的三角形与△ABC相似,则点P的坐标为(0,
)或(0,-
)或(0,
)或(0,-
).
故答案为(0,
)或(0,-
)或(0,
)或(0,-
).
 ∵B(1,0)、A(3,-3)、C(3,0),
∵B(1,0)、A(3,-3)、C(3,0),∴∠ACB=90°,CB=2,CA=3,
设P点坐标为(0,t),
∵∠POB=∠ACB=90°,
∴当
| OP |
| BC |
| OB |
| CA |
| |t| |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
当
| OP |
| CA |
| OB |
| CB |
| |t| |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
综上所述,若以O、B、P为顶点的三角形与△ABC相似,则点P的坐标为(0,
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
故答案为(0,
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.

练习册系列答案
相关题目
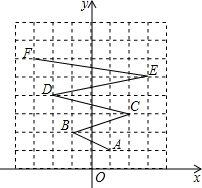 如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2014+a2015+a2016的值为(
如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2014+a2015+a2016的值为(| A、1006 | B、1007 |
| C、1509 | D、1511 |
a表示有理数,则-a一定是( )
| A、负数 | B、正数 |
| C、正数或负数 | D、以上都不对 |
 如图,△ABC和△ECD是两个全等的正三角形,△ECD可以看成是由△ABC平移得到的,其平移方向为
如图,△ABC和△ECD是两个全等的正三角形,△ECD可以看成是由△ABC平移得到的,其平移方向为 如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点O,试说明:
如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点O,试说明: 如图,已知两直线相交,∠1=30°,则∠3=
如图,已知两直线相交,∠1=30°,则∠3= 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB=
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB=