题目内容
如图,直线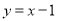 与反比例函数
与反比例函数 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(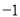 ,m).
,m).
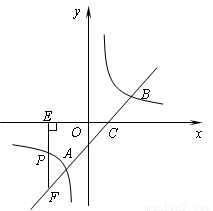
(1)求反比例函数的解析式;
(2)若点P(n,-1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
(1) ;(2)4.5.
;(2)4.5.
【解析】
试题分析:(1)将点A的坐标代入直线解析式求出m的值,再将点A的坐标代入反比例函数解析式可求出k的值,继而得出反比例函数关系式;
(2)将点P的纵坐标代入反比例函数解析式可求出点P的横坐标,将点P的横坐标和点F的横坐标相等,将点F的横坐标代入直线解析式可求出点F的纵坐标,将点的坐标转换为线段的长度后,即可计算△CEF的面积.
试题解析:(1)直线 过点A(-1,m),得m =-2
过点A(-1,m),得m =-2
反比例函数 过点A(-1,-2),得k=2
过点A(-1,-2),得k=2
所以反比例函数解析式为
(2)点P(n,-1)是反比例函数 图象上一点,所以n=-2
图象上一点,所以n=-2
当x=-2时,函数 中,y=-3
中,y=-3
当y=0时,函数 中,x=1
中,x=1
所以
考点:反比例函数与一次函数的交点问题.

练习册系列答案
相关题目
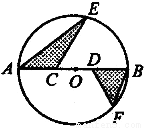

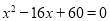 一个实数根,则该三角形的面积是( )
一个实数根,则该三角形的面积是( ) D.
D.
 三边的中点,下列说法正确的是( )
三边的中点,下列说法正确的是( ) 的面积之比为2:1
的面积之比为2:1