题目内容
三角形两边长分别是8和6,第三边长是一元二次方程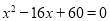 一个实数根,则该三角形的面积是( )
一个实数根,则该三角形的面积是( )
A.24 B.48 C.24或 D.
D.
B.
【解析】
试题分析:本题应先解出x的值,然后讨论是何种三角形,接着对图形进行分析,最后运用三角形的面积公式S= ×底×高求出面积.
×底×高求出面积.
试题解析:x2-16x+60=0(x-6)(x-10)=0,
∴x=6或x=10.
当x=6时,该三角形为以6为腰,8为底的等腰三角形.
∴高h= ,
,
∴S△= ×8×
×8× =
= ;
;
当x=10时,该三角形为以6和8为直角边,10为斜边的直角三角形.
∴S△= ×6×8=24.
×6×8=24.
∴S=24或 .
.
故选B.
考点:一元二次方程的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
(本题满分12分)
如图,在△ 中,∠
中,∠ >∠
>∠ ,
, ,
,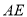 平分∠
平分∠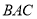 .
.
(1)若∠ =70°,∠
=70°,∠ =30°.
=30°.
①求∠ = °;②∠
= °;②∠ = °.
= °.
(2)探究:小明认为如果只要知道∠ -∠
-∠ =n°,就能求出∠
=n°,就能求出∠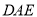 的度数?请你就这个问题展开探究:
的度数?请你就这个问题展开探究:
①实验:填表
∠ | ∠ | ∠ |
70° | 30° | (此格不需填写) |
65° | 25° | |
50° | 20° | |
80° | 56° |
②结论:当 时,试用含
时,试用含 的代数式表示∠
的代数式表示∠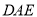 的度数,并写出推导过程;
的度数,并写出推导过程;
③应用:若∠ =56°,∠
=56°,∠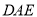 =12°,则∠
=12°,则∠ = °.
= °.



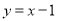 与反比例函数
与反比例函数 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(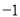 ,m).
,m).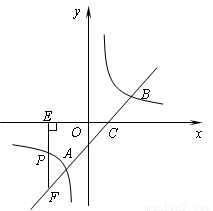
 的图象上.若点A的坐标为(-2,-2),则k的值为( )
的图象上.若点A的坐标为(-2,-2),则k的值为( )
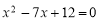 的两根,则这两个圆的位置关系是 .
的两根,则这两个圆的位置关系是 . 中,
中, ,
, ,
, 为
为 上一点,
上一点, ,
, ,求
,求 的长.
的长.