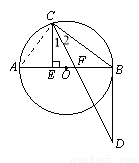
题目内容
如图,AB是⊙O的直径,点C在⊙O上,CEAB于E,CD平分ECB,交过点B的射线于D,交AB于F,且BC=BD.

(1)求证:BD是⊙O的切线;
(2)若AE=9,CE=12,求BF的长.
(2)BF=10
【解析】
试题分析:(1)根据垂直的定义可得∠CEB=90°,然后根据角平分线的性质和等腰三角形的性质,判断出∠1=∠D,从而根据平行线的判定得到CE∥BD,根据平行线的性质得∠DBA=∠CEB,由此可根据切线的判定得证结果;
(2)连接AC,由射影定理可得 ,进而求得EB的长,再由勾股定理求得BD=BC的长,然后由“两角对应相等的两三角形相似”的性质证得△EFC∽△BFD,再由相似三角形的性质得出结果.
,进而求得EB的长,再由勾股定理求得BD=BC的长,然后由“两角对应相等的两三角形相似”的性质证得△EFC∽△BFD,再由相似三角形的性质得出结果.
试题解析:(1)证明:∵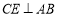 ,
,
∴ 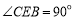 .
.
∵ CD平分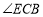 ,BC=BD,
,BC=BD,
∴  ,
, .
.
∴ 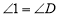 .
.
∴ 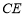 ∥
∥ .
.
∴ 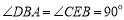 .
.
∵ AB是⊙O的直径,
∴ BD是⊙O的切线.
(2)连接AC,
∵ AB是⊙O直径,
∴ 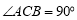 .
.
∵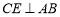 ,
,
可得  .
.
∴ 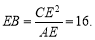
在Rt△CEB中,∠CEB=90,由勾股定理得
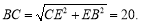
∴  .
.
∵ 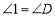 ,∠EFC =∠BFD,
,∠EFC =∠BFD,
∴ △EFC∽△BFD.
∴ 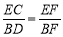 .
.
∴ 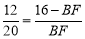 .
.
∴ BF=10.
考点:切线的判定,相似三角形,勾股定理

练习册系列答案
相关题目
 与反比例函数
与反比例函数 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(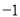 ,m).
,m).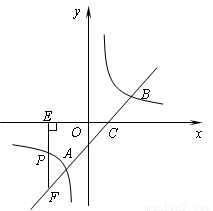
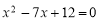 的两根,则这两个圆的位置关系是 .
的两根,则这两个圆的位置关系是 . 的解为 .
的解为 . 中,
中, ,
, ,
, 为
为 上一点,
上一点, ,
, ,求
,求 的长.
的长.



 的方程是( ).
的方程是( ). B.
B.
 D.
D.