题目内容
19.计算:(1)-22+3×(-1)4-(-4)×2;
(2)-32×(-$\frac{1}{3}$)2+($\frac{3}{4}$-$\frac{1}{6}$+$\frac{3}{8}$)×(-24);
(3)(-1)2008+(-5)×[(-2)3+2]-(-4)2÷(-$\frac{1}{2}$);
(4)3(-ab+2a)-(3a-b)+3ab;
(5)-2(ab-3a2)-[2b2-(5ba+a2)+2ab].
分析 (1)先算乘方,再算乘除,最后算加减即可;
(2)根据有理数的加减混合运算及有理数的乘法以及分配律进行计算即可;
(3)根据运算顺序,先算乘方,再算乘除,最后算加减即可;
(4)先去括号,再合并同类项即可;
(5)先去小括号,再去中括号,最后合并同类项即可.
解答 解:(1)-22+3×(-1)4-(-4)×2
=-4+3+8
=7;
(2)-32×(-$\frac{1}{3}$)2+($\frac{3}{4}$-$\frac{1}{6}$+$\frac{3}{8}$)×(-24)
=-1-18+4-9
=-24;
(3)(-1)2008+(-5)×[(-2)3+2]-(-4)2÷(-$\frac{1}{2}$)
=1+(-5)×(-6)+32
=63;
(4)3(-ab+2a)-(3a-b)+3ab
=-3ab+6a-3a+b+3ab
=3a+b;
(5)-2(ab-3a2)-[2b2-(5ba+a2)+2ab]
=-2ab+6a2-2b2+5ba+a2-2ab
=7a2-2b2+ba.
点评 本题考查了有理数的混合运算以及整式的加减,掌握有理数的运算法则和整式的加减运算是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.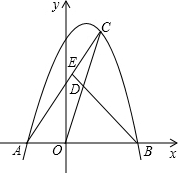 如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )
如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )
 如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )
如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
7.在四边形ABCD中,∠A、∠B、∠C、∠D的度数之比为2:3:4:3,则∠D的外角等于( )
| A. | 60° | B. | 75° | C. | 90° | D. | 120° |
4.开口向上,顶点坐标为(-9,3)的抛物线为( )
| A. | y=2(x-9)2-3 | B. | y=2(x+9)2+3 | C. | y=-2(x-9)2-3 | D. | y=-2(x+9)2+3 |
8.下列方程中是一元一次方程的是( )
| A. | 2x+3y=5 | B. | x=$\frac{1}{x}$ | C. | x2-1=0 | D. | 0.2x=1 |
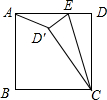 如图,正方形ABCD中,AB=4,E是边AD上一点,将△EDC沿EC翻折,点D的对应点D′落在正方形内部,若△AD′E恰是以D′E为腰的等腰三角形,那么DE的长为4$\sqrt{2}$-4或2.
如图,正方形ABCD中,AB=4,E是边AD上一点,将△EDC沿EC翻折,点D的对应点D′落在正方形内部,若△AD′E恰是以D′E为腰的等腰三角形,那么DE的长为4$\sqrt{2}$-4或2.