题目内容
10.解方程(组)(1)$\frac{y-2}{4}$-$\frac{2y-1}{6}$=1
(2)$\left\{\begin{array}{l}{x+2y=3}\\{2x-3y=13}\end{array}\right.$.
分析 (1)方程去分母,去括号,移项合并,把y系数化为1,即可求出解;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)去分母得:3y-6-4y+2=12,
移项合并得:-y=16,
解得:y=-16;
(2)$\left\{\begin{array}{l}{x+2y=3①}\\{2x-3y=13②}\end{array}\right.$,
①×2-②得:7y=-7,
解得:y=-1,
把y=-1代入①得:x=5,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$.
点评 此题考查了解一元一次方程,以及解二元一次方程组,解一元一次方程的步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.-3的相反数是( )
| A. | -$\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{3}$ | D. | -3 |
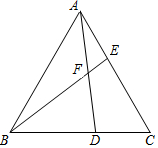 如图,点D、E分别在等边△ABC的边BC、AC上,且AE=CD,AD与BE相交于点F,则∠BFD的度数为60°.
如图,点D、E分别在等边△ABC的边BC、AC上,且AE=CD,AD与BE相交于点F,则∠BFD的度数为60°.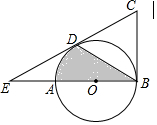 如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.