题目内容
15．
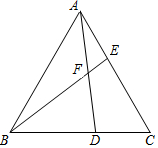如图，点D、E分别在等边△ABC的边BC、AC上，且AE=CD，AD与BE相交于点F，则∠BFD的度数为60°．
分析 证明△ABE≌△CAD，推出∠ABE=∠CAD，由∠BFD=∠ABE+∠BAF=∠CAD+∠BAF=60°，即可解决问题．
解答 证明：∵△ABC是等边三角形，
∴∠BAE=∠C=60°，AB=AC，
在△ABE和△CAD中，
$\left\{\begin{array}{l}{AB=CA}\\{∠BAE=∠C}\\{AE=CD}\end{array}\right.$，
∴△ABE≌△CAD，
∴∠ABE=∠CAD，
∵∠BFD=∠ABE+∠BAF=∠CAD+∠BAF=60°，
故答案为60°
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
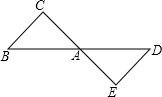如图，△ABC与△ADE关于点A成中心对称．
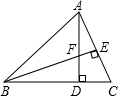如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为点D，E，AD与BE相交于点F，若BF=AC，则∠ABC=45°．