题目内容
6. 教练对明明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系满足y=a(x-4)2+h.
教练对明明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系满足y=a(x-4)2+h.(1)在某次比赛中,他第一次投掷后,铅球的最大高度为3m,落地点距离出手点的水平距离为10m,求他的出手高度是多少m?
(2)第二次投掷时,他加大了力度,奋力一掷,结果出手点高度变为2m,铅球行进的最大高度增加了0.6m,求他这次投掷后的落地点距离出手点的水平距离.
(3)若第三次投掷后,落地点距离出手点的距离为12,他便可以获得冠军.如果出手高度仍为2m,则铅球行进过程中的最大高度为多少m?
分析 (1)利用铅球的最大高度为3m,得出h=3,进一步代入(10,0)求得a,得出函数解析式,令x=0,得出他的出手高度即可;
(2)铅球的最大高度为3.6m,得出h=3.6,进一步代入(0,2)求得a,得出函数解析式,令y=0,得出他的投掷后的落地点距离出手点的水平距离即可;
(3)把点(0,2),(12,0)代入y=a(x-4)2+h得函数解析式,进一步求得最值即可.
解答 解:(1)由题意可知:h=3,
y=a(x-4)2+3,
代入(10,0)解得a=-$\frac{1}{12}$,
则y=-$\frac{1}{12}$(x-4)2+3,
令x=0,则y=$\frac{5}{3}$.
答:他的出手高度是$\frac{5}{3}$m;
(2)由题意可知:y=a(x-4)2+3.6,
代入(0,2)解得a=-$\frac{1}{10}$,
则y=-$\frac{1}{10}$(x-4)2+3.6,
令y=0,解得x=10,
答:他这次投掷后的落地点距离出手点的水平距离是10m;
(3)把(0,2),(12,0)代入y=a(x-4)2+h得
$\left\{\begin{array}{l}{16a+h=2}\\{64a+h=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{24}}\\{h=\frac{8}{3}}\end{array}\right.$,
则y=-$\frac{1}{24}$(x-4)2+$\frac{8}{3}$.
答:铅球行进过程中的最大高度为$\frac{8}{3}$m.
点评 此题考查二次函数的实际运用,掌握待定系数法和顶点式求最值是解决问题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
15.在Rt△ABC中,AD为斜边上的高,S△ABC=4S△ABD,则cosB=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{\sqrt{3}}{2}$ |
 如图,梯形ABCD绕O点旋转后,顶点C的对应点为C′点,试确定顶点A,B,D对应点的位置,以及旋转后的梯形A′B′C′D′.
如图,梯形ABCD绕O点旋转后,顶点C的对应点为C′点,试确定顶点A,B,D对应点的位置,以及旋转后的梯形A′B′C′D′.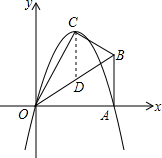 如图,已知点A (2$\sqrt{3}$,0)、B(2$\sqrt{3}$,2).将△OAB沿OB折叠后,点A落在点c处,抛物线经过O、A、C三点,其对称轴与OB交于点D.
如图,已知点A (2$\sqrt{3}$,0)、B(2$\sqrt{3}$,2).将△OAB沿OB折叠后,点A落在点c处,抛物线经过O、A、C三点,其对称轴与OB交于点D. 如图,已知梯形ABCD中,∠A=∠B=90°,AB=AD=12cm,BC=21cm,CD=15cm,E是AD上的点,AE=8cm.
如图,已知梯形ABCD中,∠A=∠B=90°,AB=AD=12cm,BC=21cm,CD=15cm,E是AD上的点,AE=8cm.