题目内容
8.已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=36°,则∠OGA=18°.
(2)若∠GOA=$\frac{1}{3}$∠BOA,∠GAD=$\frac{1}{3}$∠BAD,∠OBA=36°,则∠OGA=12°.
(3)将(2)中“∠OBA=36°”改为“∠OBA=β”,其余条件不变,则∠OGA=$\frac{1}{3}β$(用含β的代数式表示).
(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=β(30°<β<90°)求∠OGA的度数(用含β的代数式表示).

分析 (1)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;
(2)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;
(3)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;
(4)讨论:当∠EOD:∠COE=1:2时,利用∠BAD=∠ABO+∠BOA=β+90°,∠FAD=∠EOD+∠OGA得到2×30°+2∠OGA=β+90°,则∠OGA=$\frac{1}{2}β$+15°;当∠EOD:∠COE=2:1时,则∠EOD=60°,同理得∠OGA=$\frac{1}{2}β$-15°.
解答 解:(1)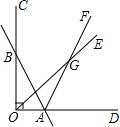 ∵∠BOA=90°,∠OBA=36°,
∵∠BOA=90°,∠OBA=36°,
∴∠BAD=∠BOA+∠ABO=126°,
∵AF平分∠BAD,OE平分∠BOA,∠BOA=90°,
∴∠GAD=$\frac{1}{2}$∠BAD=63°,∠EOA=$\frac{1}{2}$∠BOA=45°,
∴∠OGA=∠GAD-∠EOA=63°-45°=18°;
故答案为18°;
(2)∵∠BOA=90°,∠OBA=36°,
∴∠BAD=∠BOA+∠ABO=126°,
∵∠BOA=90°,∠GOA=$\frac{1}{3}$∠BOA,∠GAD=$\frac{1}{3}$∠BAD
∴∠GAD=42°,∠EOA=30°,
∴∠OGA=∠GAD-∠EOA=42°-30°=12°;
故答案为12°;
(3)∵∠BOA=90°,∠OBA=β,
∴∠BAD=∠BOA+∠ABO=90°+β,
∵∠BOA=90°,∠GOA=$\frac{1}{3}$∠BOA,∠GAD=$\frac{1}{3}$∠BAD
∴∠GAD=30°+$\frac{1}{3}β$,∠EOA=30°,
∴∠OGA=∠GAD-∠EOA=$\frac{1}{3}$β,
故答案为:$\frac{1}{3}$β;
(4)当∠EOD:∠COE=1:2时,
则∠EOD=30°,
∵∠BAD=∠ABO+∠BOA=β+90°,
∵AF平分∠BAD,
∴∠FAD=$\frac{1}{2}$∠BAD,
∵∠FAD=∠EOD+∠OGA,
∴2×30°+2∠OGA=β+90°,
∴∠OGA=$\frac{1}{2}$β+15°;
当∠EOD:∠COE=2:1时,则∠EOD=60°,
同理得到∠OGA=$\frac{1}{2}β$-15°,
即∠OGA的度数为$\frac{1}{2}β$+15°或$\frac{1}{2}β$-15°.
点评 本题考查了三角形内角和定理:三角形内角和为180°.也考查了三角形外角性质.

 如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )
如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
 如图,△OAB和△ACD是等边三角形,O、A、C在x轴上,B、D在y=$\frac{\sqrt{3}}{x}$(x>0)的图象上,则点C的坐标是( )
如图,△OAB和△ACD是等边三角形,O、A、C在x轴上,B、D在y=$\frac{\sqrt{3}}{x}$(x>0)的图象上,则点C的坐标是( )| A. | (-1+$\sqrt{2}$,0) | B. | (1+$\sqrt{2}$,0) | C. | (2$\sqrt{2}$,0) | D. | (2+$\sqrt{2}$,0) |
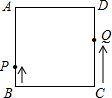 已知正方形ABCD中,AB=BC=CD=AD=10cm,动点P,Q分别从点B,C同时出发沿正方形的四周运动.设点P的运动速度为2cm/s,点Q的运动速度为3cm/s,设点P,Q运动的时间为t(s)
已知正方形ABCD中,AB=BC=CD=AD=10cm,动点P,Q分别从点B,C同时出发沿正方形的四周运动.设点P的运动速度为2cm/s,点Q的运动速度为3cm/s,设点P,Q运动的时间为t(s) 如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽.
如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽.
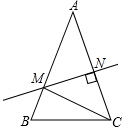 如图,在等腰△ABC中,∠A=40°,AC的垂直平分线MN交AB,AC于点M,N.则∠MCB=30°.
如图,在等腰△ABC中,∠A=40°,AC的垂直平分线MN交AB,AC于点M,N.则∠MCB=30°. 列方程解应用题.
列方程解应用题.