题目内容
11.如图是2017年1月份的日历.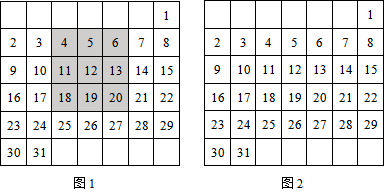
(1)图1中,带阴影的方框中的9个数的和与方框正中心的数有什么倍数关系?
(2)在图2中,将带阴影的方块移动,任意框出9个数(每个格子都有数字),(1)中的结论还成立吗?请说明理由;
(3)带阴影的方框移动过程中,9个数的和可以是135吗?若可以,求出方框正中心的数;若不可以,请说明理由.
分析 (1)求出方框中9个数的和,再除以方框正中心的数即可得出结论;
(2)设最中间的数为x,写出按顺序写出方框中的9个数,将其相加即可得出结论;
(3)设最中间的数为y,由(2)结合9个数的和为135即可得出关于y的一元一次方程,解之即可得出y值,对照图形即可得出不可以.
解答 解:(1)∵(4+5+6+11+12+13+18+19+20)÷12=9,
∴方框中的9个数的和是方框正中心的数的9倍.
(2)成立,理由如下:
设最中间的数为x,则9个数字如图所示:
这9个数的和为:(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x,
∴方框中的9个数的和是方框正中心的数的9倍.
(3)不可以,理由如下:
设最中间的数为y,则9y=135,
解得:y=15,
∵图中不存在以数字15为最中间的数的方框,
∴不可以.
点评 本题考查了一元一次方程的应用以及代数式求和,利用代数式的加法找出方框中的9个数的和是方框正中心的数的9倍是解题的关键.

练习册系列答案
相关题目
2.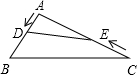 如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
 如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )| A. | 2.5秒 | B. | 4.5秒 | C. | 2.5秒或4.5秒 | D. | 2.5秒或4秒 |
3.若关于x的方程(m-2)x2+mx-1=0是一元二次方程,则m的取值范围是( )
| A. | m≠2 | B. | m=2 | C. | m≥2 | D. | m≠0 |
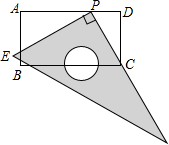 如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,则当x<0时,y随x的增大而增大.(填“增大”或“减小”)
已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,则当x<0时,y随x的增大而增大.(填“增大”或“减小”)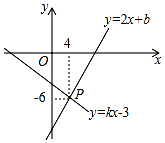 如图,已知一次函数y=2x+b和y=kx-3(k≠0)的图象交于点P,则二元一次方程组$\left\{\begin{array}{l}2x-y=-b\\ kx-y=3\end{array}\right.$的解是$\left\{\begin{array}{l}{x=4}\\{y=-6}\end{array}\right.$.
如图,已知一次函数y=2x+b和y=kx-3(k≠0)的图象交于点P,则二元一次方程组$\left\{\begin{array}{l}2x-y=-b\\ kx-y=3\end{array}\right.$的解是$\left\{\begin{array}{l}{x=4}\\{y=-6}\end{array}\right.$.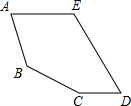 聪聪用五根宽度相同的木条拼成了一个五边形,如图所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.
聪聪用五根宽度相同的木条拼成了一个五边形,如图所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.