题目内容
7.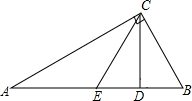 已知:如图,在△ABC中,∠A=30°,∠ACB=90°,E、D分别是AB、EB中点.求证:CD⊥AB.
已知:如图,在△ABC中,∠A=30°,∠ACB=90°,E、D分别是AB、EB中点.求证:CD⊥AB.证明:∵∠A=30°,∠ACB=90°
∴BC=$\frac{1}{2}$AB(直角三角形中,30°所对的直角边是斜边的一半)
又∵E是AB中点
∴CE=$\frac{1}{2}$AB(直角三角形斜边上的中线等于斜边的一半)
∴CE=CB
又∵D是EB中点
∴CD⊥AB(等腰三角形三线合一)
分析 根据直角三角形中,30°所对的直角边是斜边的一半、直角三角形斜边上的中线等于斜边的一半得到CE=CB,根据等腰三角形的性质证明即可.
解答 证明:∵∠A=30°,∠ACB=90°
∴BC=$\frac{1}{2}$AB(直角三角形中,30°所对的直角边是斜边的一半)
又∵E是AB中点
∴CE=$\frac{1}{2}$AB(直角三角形斜边上的中线等于斜边的一半),
∴CE=CB,
又∵D是EB中点,
∴CD⊥AB(等腰三角形三线合一),
故答案为:BC;直角三角形中,30°所对的直角边是斜边的一半;CE;$\frac{1}{2}$AB;直角三角形斜边上的中线等于斜边的一半;CE;CB;等腰三角形三线合一.
点评 本题考查的是直角三角形的性质和等腰三角形的性质,掌握直角三角形中,30°所对的直角边是斜边的一半、直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某摩托车厂本周计划每日生产250辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日产量与计划产量相比情况如下:
(1)本周六生产了多少辆?
(2)本周生产总量与计划生产量相比是增产还是减产?增产或减产几辆?
(3)产量最多的一天比产量最少的一天多生产多少辆?
| 星 期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增 减 | -5 | +10 | -3 | +4 | +6 | -8 | -6 |
(2)本周生产总量与计划生产量相比是增产还是减产?增产或减产几辆?
(3)产量最多的一天比产量最少的一天多生产多少辆?
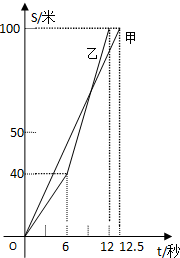 甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:
甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:
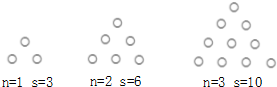 如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.
如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.